Understanding Geometry as Layered Data

The end of the basics series

---

This article is part of the basics of Computational Design series. Even if you don’t use Grasshopper or Dynamo every day, understanding the fundamentals can help you spot where they might be useful in your work.

Part 1 : The three vital numbers in computational design

Part 2 : A Beginner’s Guide to Curves in Computational Design

Part 3 : How Surfaces Really Work in Rhino and Why That Matters

Part 4 : What Are B-reps in Rhino, and Why Do They Matter?

Part 5 : A Simple Guide to Meshes in Computational Design

Part 6 : Understanding Geometry as Layered Data (here)

---

I might be OCD. Okay, I'm not. But it sure feels that way sometimes because I like things organized.

Luckily for me, there's this concept in software development called "object-oriented" design that backs me up. The idea is pretty simple. It's about grouping things that belong with each other. It's like putting all your kid's toys in a box.

This idea of grouping things just makes sense. It actually mirrors the way we think. Like keeping cumin and cinnamon next to each other on the spice rack, not in different cupboards across the kitchen. I like this idea too because my whole work philosophy of being intentional is about being organized and clear about things.

So why am I telling you all of this ?

Because over the past few weeks, we’ve explored the common geometry types in computational design, especially in Rhino and Grasshopper. And now, it’s time to put the pieces back and see how they all fit together.

I know some of these posts might’ve felt dry. Maybe even pointless if you don’t work with geometry often. But these types, points, lines, surfaces, and so on, are the foundation for computational design. It's like cooking in someone else's kitchen, before you can make anything, you need to know what you’ve got, where it lives and what you can do with it.

So today's the recap. Let's put everything in perspective.

Geometry as data types

I've hinted at this before, but avoided saying the word "data" until now. I wanted each geometry type to stand on its own first. But really, it’s all just 1s and 0s and that’s what the computer understands. What matters is how we organize and use those 1s and 0s.

A point is just three points with some other properties that the Rhino needs. A curve is just a list of those points. Everything is grouped by similarity, then layered on top of one another to build more complex geometry. It's an elegant way to layer in complexity.

The reason this is important is because it changes the way we see geometry. It isn't some mysterious or intimidating thing, it's just structured data. Yes, there is math involved. Yes, it's quite technical. But really it's simple data like numbers built on top one another. Like a cake. A somewhat technical and mathematical cake.

The geometry types we’ve covered

Here’s what we’ve looked at:

• Points

• Lines

• Curves

• Surfaces

• Breps

• Meshes

Let’s run through them one last time, this time with a more data-oriented lens

Points

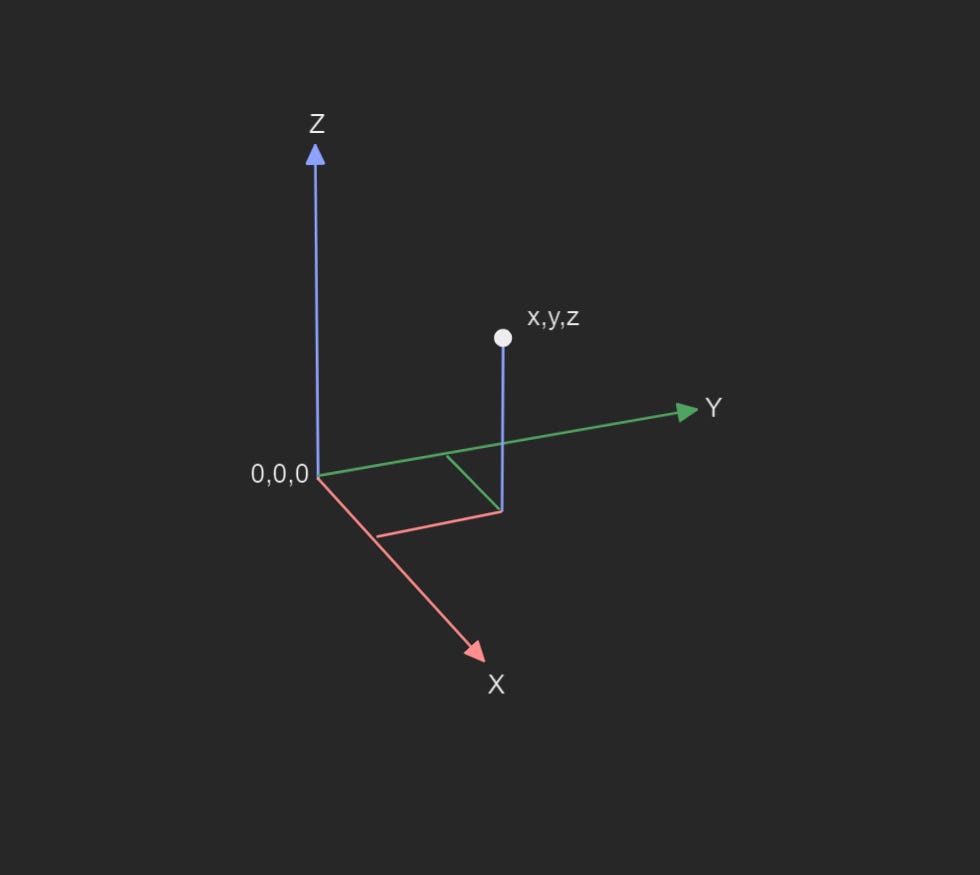
Points are locations in 3D space. They have an X, Y, and Z coordinate, usually relative to an origin (0,0,0). From a data perspective, they’re just three numbers. That’s why you can treat colours or vectors as "points".

You can even use the X and Y coordinates for position and let the Z represent something else, like intensity or some custom value. Once you see points this way, they become incredibly flexible.

Full article on points here

Lines

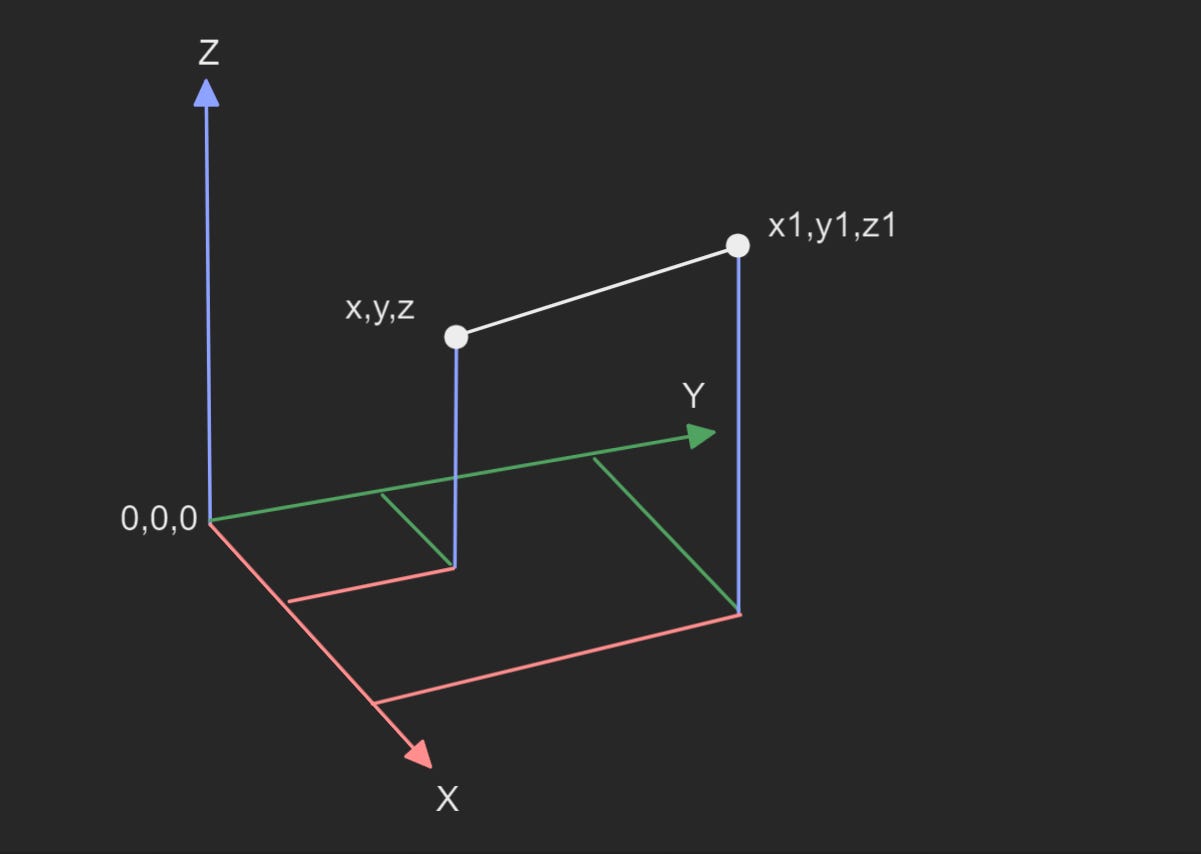
Then we can start building on the points. Connect two of them and you form a line, which let's us do a lot more. We can get directions, measurements, perform intersections, etc. Also, when we combine multiple lines, we get polylines. Which let's us represent more complex shapes.

From a data perspective, a line is really just two points. And that's why you can treat a line like a vector. If a vector goes from 0,0,0 to a point. Then a line is the vector from it's start to it's end point. That’s actually why in Grasshopper, you can plug a Line component into a Vector component and it still works.

Full article on lines here

Curves

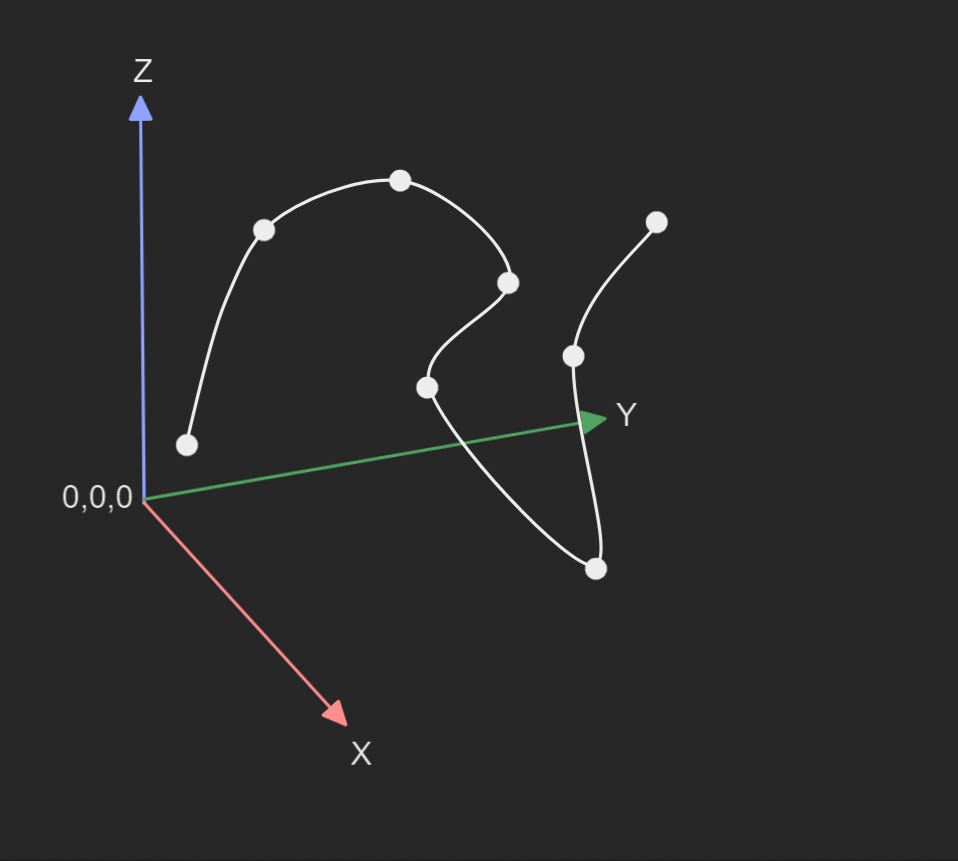
A more complex way to connect points is through curves. They're like lines, but with more math involved. Instead of a direct connection, curves interpolate between points using equations. This introduces new properties like tangents and curvatures.

When you place points in a specific order and connect them in a certain way, you get shapes: rectangles, arcs, circles, and so on. Rhino even gives you built-in ways to create these shapes, though under the hood, they’re still just curves. I.e. you can use dimensions to create these shapes instead of moving points around.

Full article on curves here

Surfaces

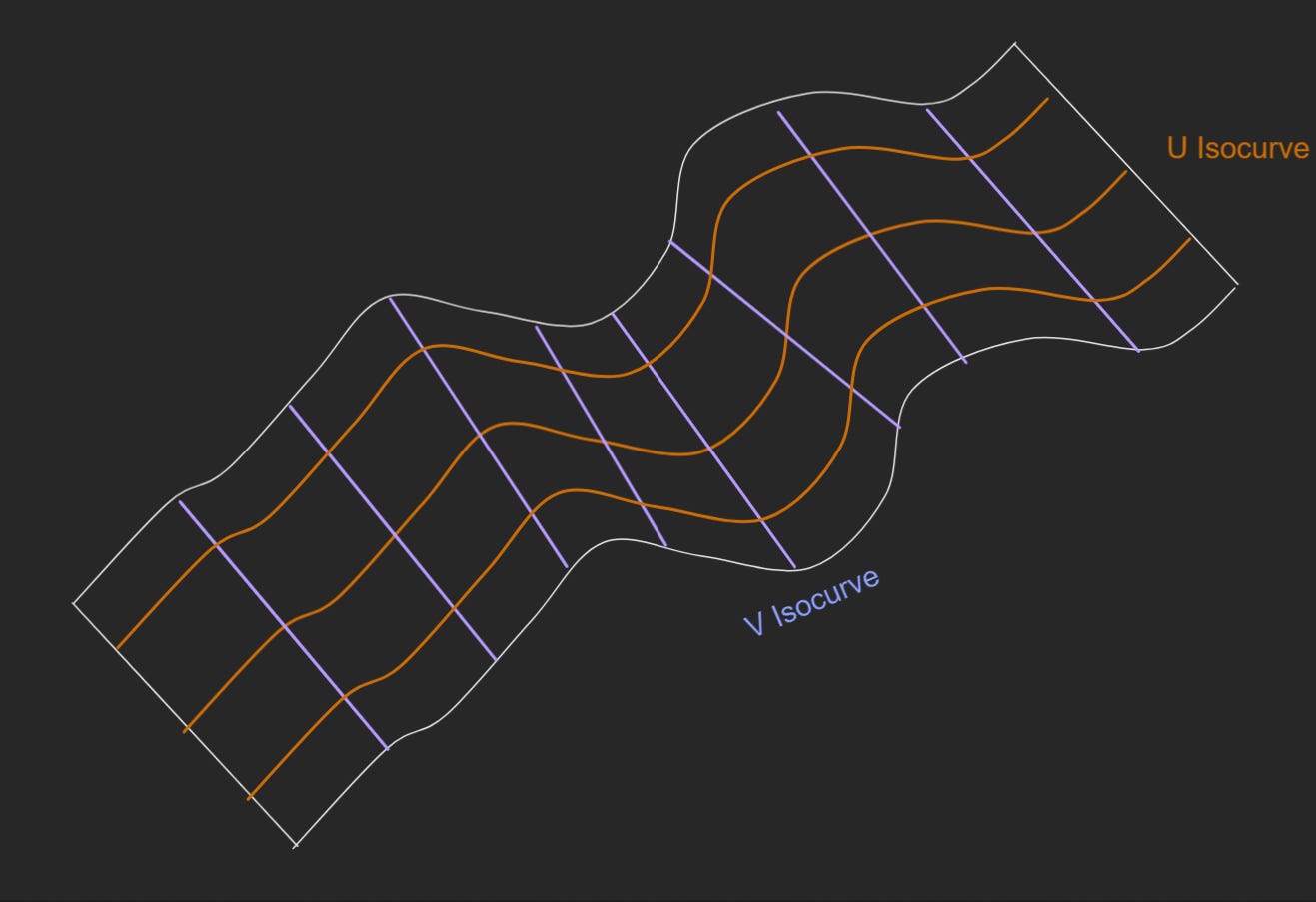
Okay, let's go deeper. Now, connect curves in two directions and you get a surface.

And again, we gain more properties and data to play with. Now we can perform more complex boolean operations, like intersections, unions, and differences. We can extract planes and normal vectors. We can even start to see how this virtual geometry begins to resemble what we see in the real world.

Full article on surfaces here

B-reps

Just like we combined lines to get polylines, we can combine two or more surfaces to get a B-rep. Which is Rhino’s (and a few other CAD programs) term for a poly-surface or “solid.”

This is where the idea of geometry as data becomes even more obvious. A closed B-rep is really just a collection of surfaces that share edges. But Rhino treats them as a solid. It can calculate volumes, apply fillets, and perform solid operations, even though it’s just working with joined surfaces.

Full article on B-reps here

Meshes

When it comes to thinking about geometry as data, meshes are the best example. They’re one of the most performance-friendly geometry types. It uses the least amount of data to represent geometry. With just points and lines, you can represent almost any shape.

That’s why you’ll see meshes everywhere. They’re faster, lighter, and more efficient than B-reps, especially when dealing with large models or simulations.

Full article on meshes here

P.S. Get my free guide on how to apply computational design to your work here.

Geometry is a way of organizing data

All of this, points, curves, B-reps, meshes, is a just a hierarchy of data. It builds on the one before it. Like a geometry layer cake. And the more structured the data, the more things we can do with it. It's an elegant way of organizing numbers.

Of course, like any structure, too much complexity can become a burden. It's like comparing a simple house key to a 15 step alarm system. The alary system is definitely more secure but what happens if you lose power? Or you forget the code? Now you’ve got to reset the system or call someone or wish you never had an alarm in the first place. With a key, you just grab the spare.

It's the same with geometry, mess up a point and you just have to re-enter three numbers. A B-rep or a mesh though, recreating them takes a lot more effort.

A quick word on “data” data

There’s another layer here, one that I have avoided for good reason. It's the data types that aren’t geometric.

• Numbers

• Text

• Booleans (true/false)

These are what your geometry is made from. And I didn't elaborate on them because they are things you don’t need unless you’re working with more than just geometry. To me, these sit just outside the “basics.” If geometry is your starting point, these are what you’ll likely encounter next, especially if you find yourself working with both data and geometry at the same time (which, in my case, is most of the time).

The end of the “basics”

When I think of “basics,” I think of high-level ideas that let you actually get started.

Side note: I don’t like labeling things as “basic” or “intermediate”. People come into computational design with very different backgrounds, so what’s foundational for one person might be too advanced for someone else, you just never know.

You don’t need to know the difference between a float and an integer unless you’re deep in the weeds. And by that point, the geometry types should already feel second nature.

But you should know what a point is. How a surface behaves. Why a mesh might be better for performance, even if it’s harder to edit.

This series is meant to give you that. A top-down view of what’s essential for working with geometry in computational design. I hope it delivered on that.

I'll be working on an "intermediate" level series next, one that builds on top of this and introduces more "data" data concepts.

Thanks for sticking with me.

– Braden

Thank you for reading. Consider subscribing if you haven’t, it really helps me know my writing here is useful.