A Beginner's Guide to Curves
This article is part of the basics of Computational Design series. Even if you don’t use Grasshopper or Dynamo every day, understanding the fundamentals can help you spot where they might be useful in your work.
Part 1 : The three vital numbers in computational design
Part 2 : A Beginner’s Guide to Curves in Computational Design (here)
Part 3 : How Surfaces Really Work in Rhino and Why That Matters
Part 4 : What Are B-reps in Rhino, and Why Do They Matter?
I used to hate high school math. I was really good at it but I couldn't see the point. I mean why would a 14 year old need to know about algebra or differentiation ? I only did it so my parents wouldn't yell at me.
I got lucky though, my dad was an engineer and for most of my life I knew that is what I wanted to be. But even during my engineering degree, I still didn’t get it. The math was more complicated and there was hints of how it useful it was but it was still abstract to me. It all still felt like a necessary evil to getting a degree. Why bother learning about curves when the software handles it for us anyway?
It wasn't until about 5 years ago when I got into Grasshopper, that things started to make way more sense. Working with geometry every day made me realize how useful the math was. It made me understand that what defines an object matters more than how it looks. You can have a model that looks perfect on screen but is unusable once you try to work with it.
In computational design, especially when working with tools like Grasshopper, understanding how curves behave is essential. You start to see that geometry is more than just appearance and aesthetics, it’s about definition, and control.
So since we’ve already looked at points, it’s time we see at how they connect.
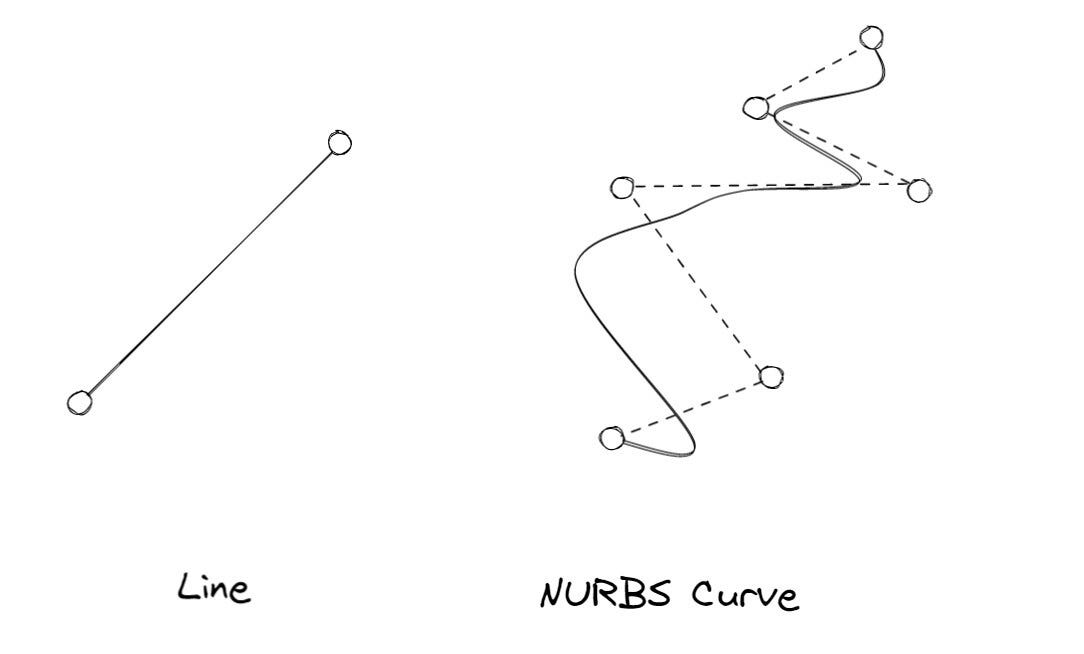
What is a curve ?
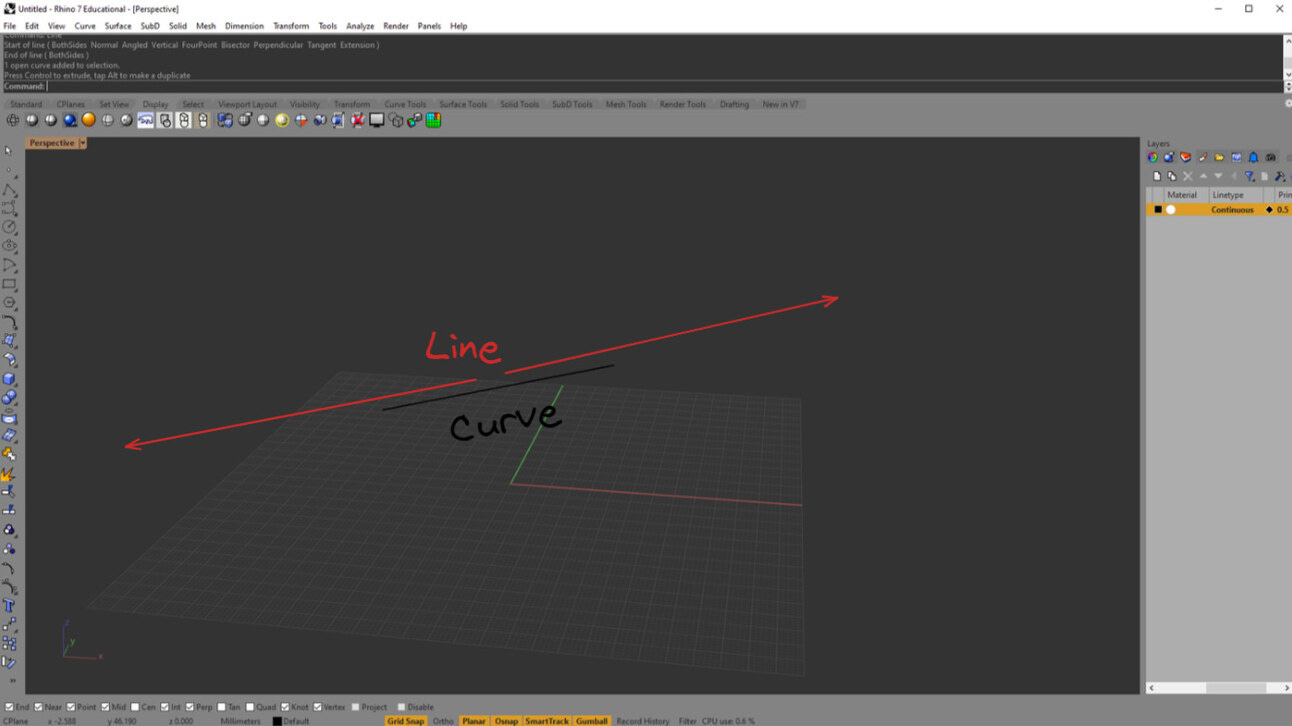
To put it simply, a curve is just a connection between two or more points. That can be a straight line (direct connection from A to B), or something more "curvy", like a NURBS curve with multiple control points.
Programs like Grasshopper or Dynamo make curve creation feel easy. Give it some points and the software handles the math for you. But if you want to model precisely (and/or cleanly), you’ll need to understand how those curves behave and what they are made of.
The degrees of a curve
If you're just getting into modelling, the good news is that you don’t need to understand all the math behind curves. But if you want clean, useful models, you at least need to understand what the degree of a curve does.
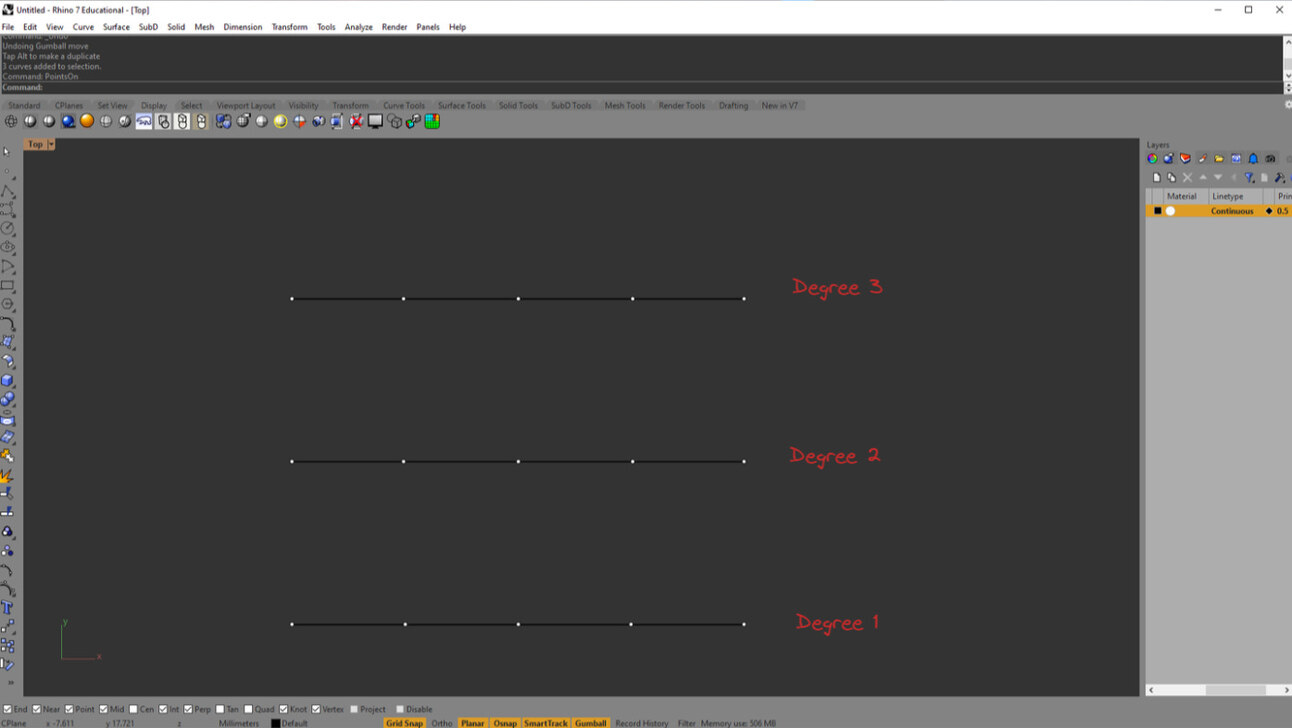
Using Rhino, we can see this in action. Let's say I have three curves through 5 points. Each curve has a different degree: 1,2 and 3.
Now, when we shift the middle point upwards, we'll see the affect the degree has on a curve.
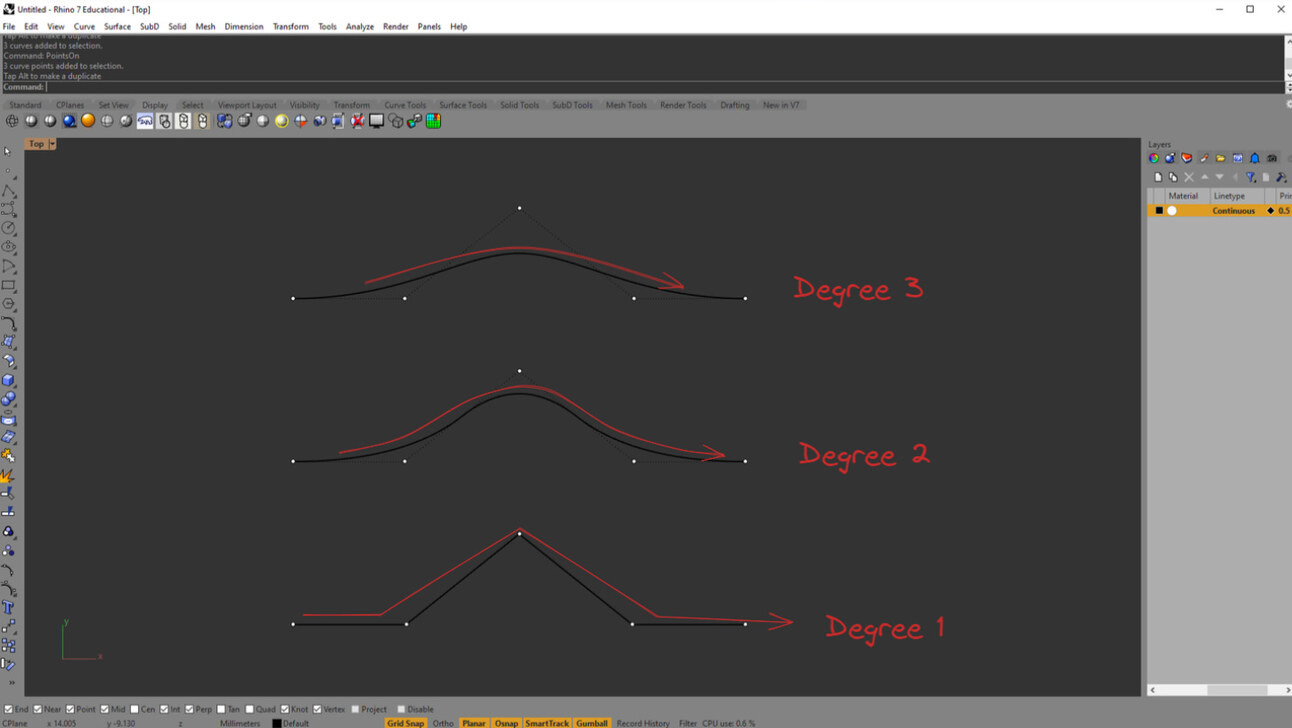
Notice how the degree changes the way the curve flows between points
The degree 1 curve (a polyline) connects straight from point to point—no smoothness at all.
The degree 2 and 3 curves begin to "flow" through the space instead of touching the points. Those points have now become control points, meaning the curve is influenced by them but doesn’t necessarily pass through them. In modelling terms, any curve that has a high degree (>2) is known as a smooth curve.
So, if you need the curve to pass through specific points, like dimensions on a drawing, you’ll need to account for that when creating your curve.
Note: There’s a lot more math behind curves. Tangents, Knots, Continuity, etc. but the degree covers 80% of what you need to know in practice. As you become more experience, you definitely need to know more about curves, perhaps I'll cover that in another article
Curve Types in programs
Modern software goes beyond just letting you draw "a curve." It categorizes curves into types, giving you tools for easier creation and editing.
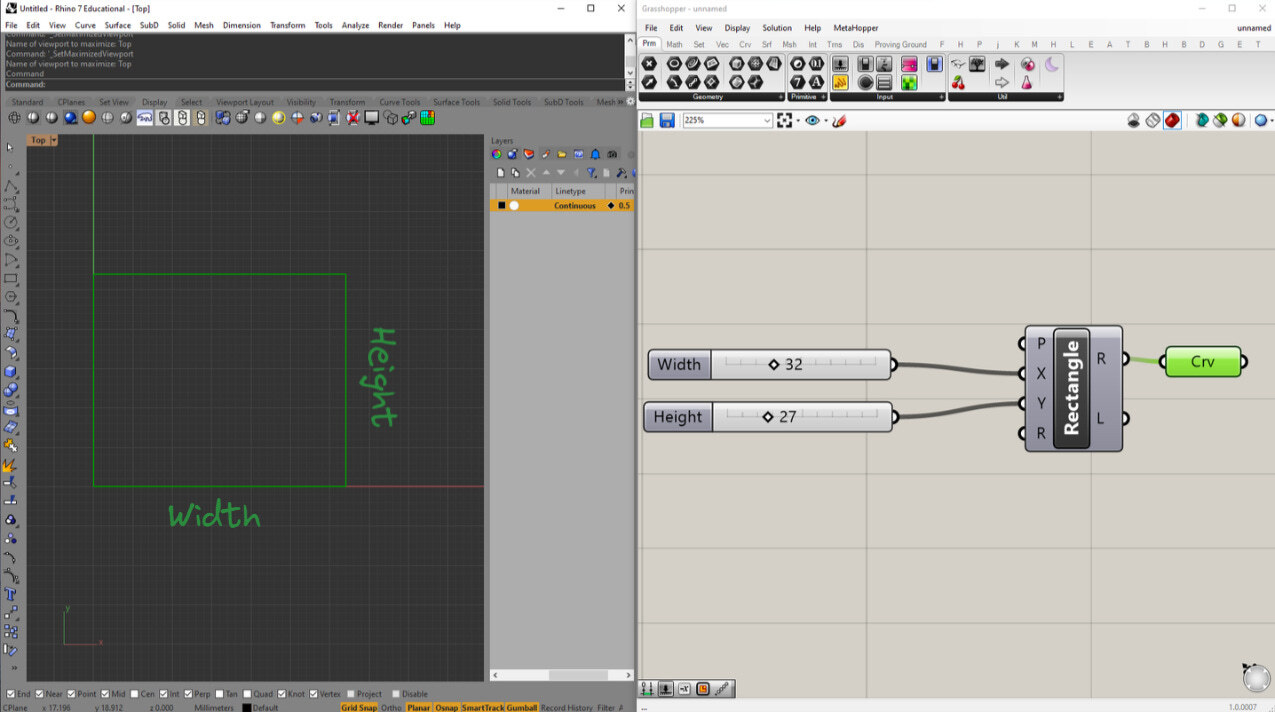
Instead of drawing four lines each time you want a rectangle, most modern programs like Rhino will let you define a rectangle with it's dimensions.
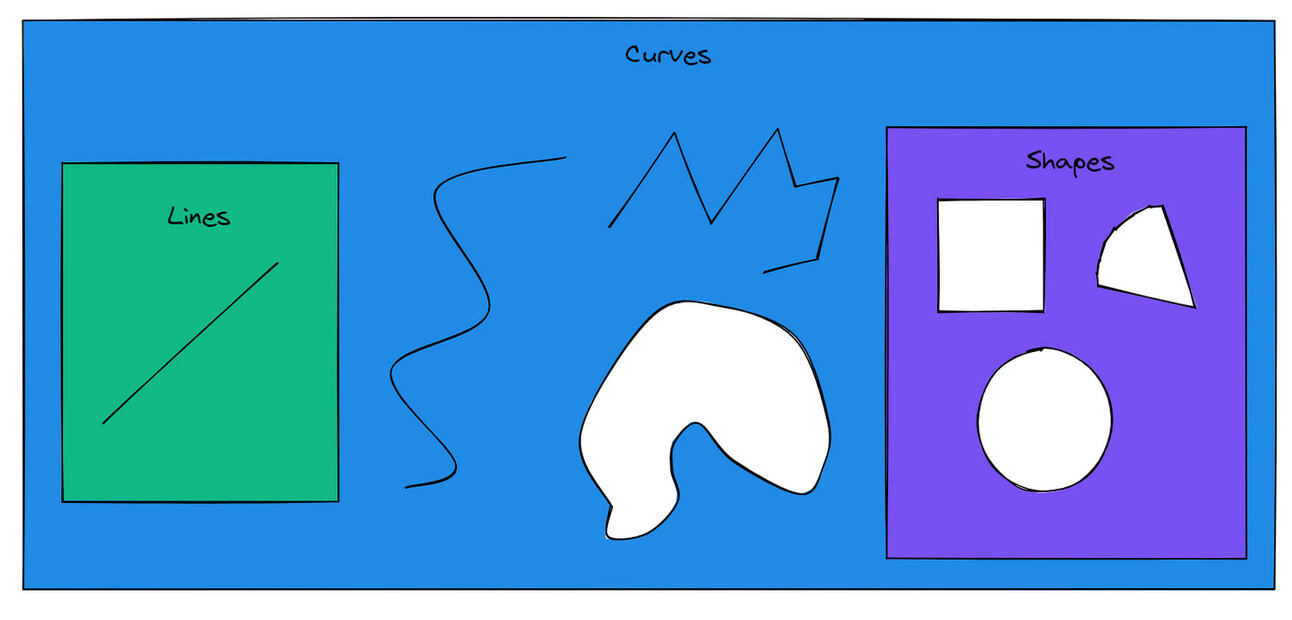
Lines and Polylines
The simplest curve. Just a connection between two points. And a series of lines joined together is called a polyline. Even though lines are simple, don’t underestimate it because they are a very useful tool. Lines are mathematically infinite, which makes them perfect for operations like intersections or projections.
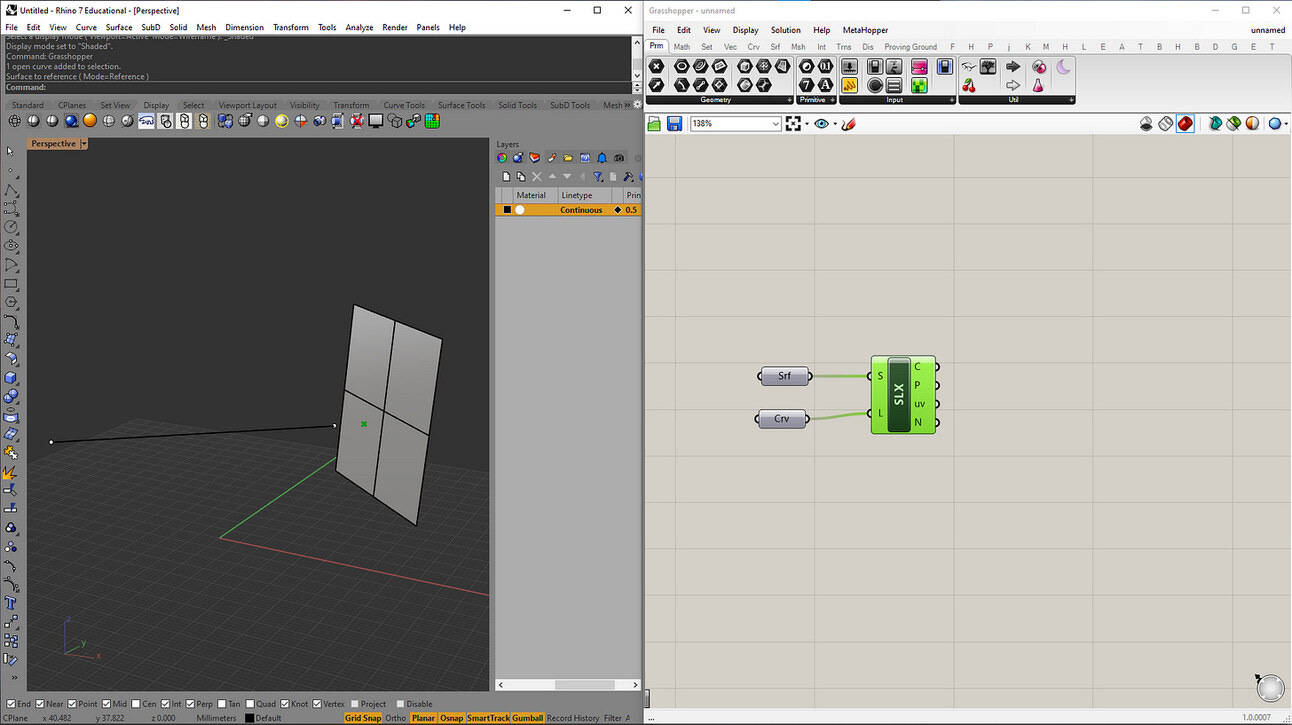
Like in Grasshopper, you can use the Line|Surface component to figure out if it intersects with a surface.
Intersections are key to accurate modeling, and lines are essential for finding them.
Shapes
Shapes like rectangles, circles, arcs, and ellipses are just closed curves with known dimensions. Instead of redrawing four lines every time you want a rectangle, you can just specify width and height.
They’re great when you want reusable and well-defined geometry. There are also functions in Grasshopper and Rhino that let you try and fit curves to shapes. Like fitting a curve that is not quite circular to a circle. They're advanced techniques but useful when trying to rationalize geometry.
Curves
And everything else falls under this category. Technically, lines and shapes are also curves, but calling something a "curve" usually means it’s freeform and defined by control points.
Grasshopper makes this distinction clear, with components that behave differently depending on the curve type.
What makes a clean curve ?
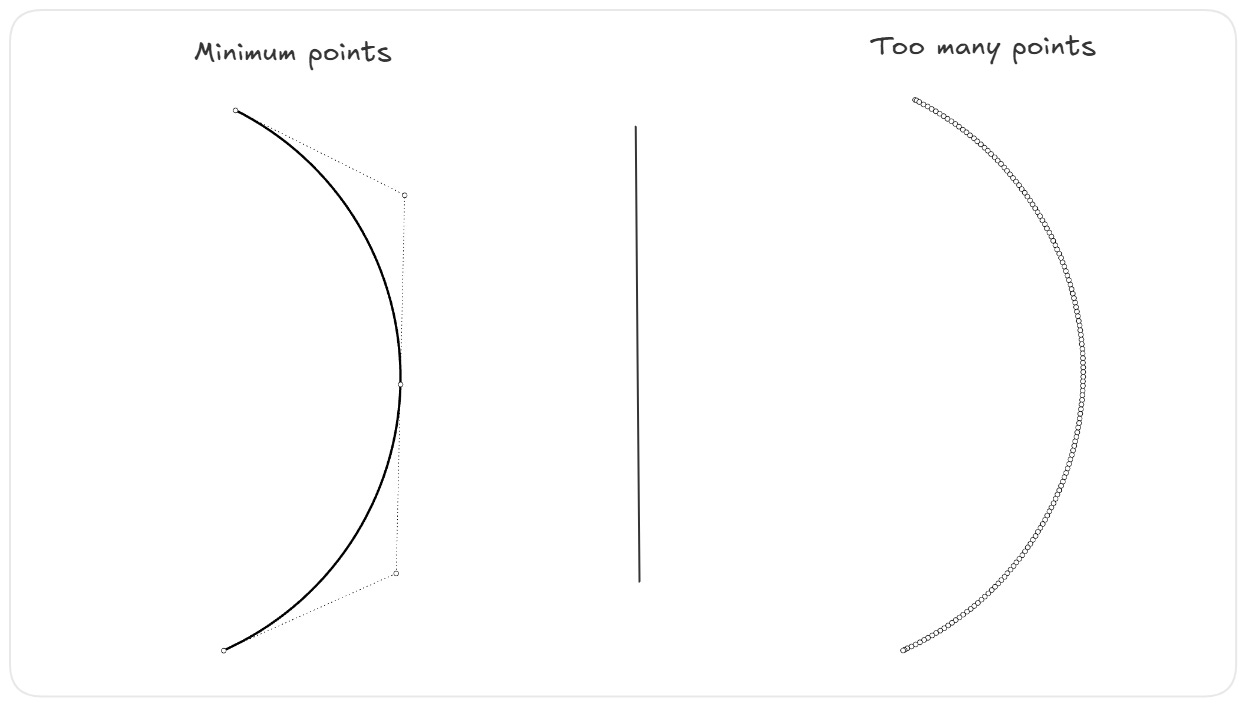
Anyone can draw a curve that looks right. But in computational design, that’s not enough. A clean curve is one that:
Uses the minimum number of control points needed
Has a consistent and intentional degree
Is easy to edit or manipulate later
Sure, you can brute-force your way to a nice-looking curve by adding lots of control points. But it makes the model harder to work with and introduces problems later down the line.
Clean curves are easier to edit, easier to analyze, and more likely to behave the way you expect when you use them in scripts or automation workflows.
Final Thoughts
Curves are everywhere in computational design. Whether you're making roads, facades, duct routes, or rebars, you’re working with curves. Understanding how they behave: what defines them, how degrees affect them, how to model them cleanly, and more, is foundational knowledge.
It’s easy to let the software do the work for you. But if you want more control and to create cleaner and better geometry, this is the beginning. There’s a lot more to curves than what we’ve covered here. But this is a solid starting point and you’ll be surprised how far this foundation can take you.
Thanks for reading.
If you’ve enjoyed that, consider subscribing to get more articles like these delivered to you. It also helped support the work I do. You’ll also get a gift as a thank you for signing up