An Introduction to Points and Vectors
This article is part of a new series on the basics of Computational Design. Even if you don’t use Grasshopper or Dynamo daily, understanding the fundamentals can help you spot opportunities to use them at work.
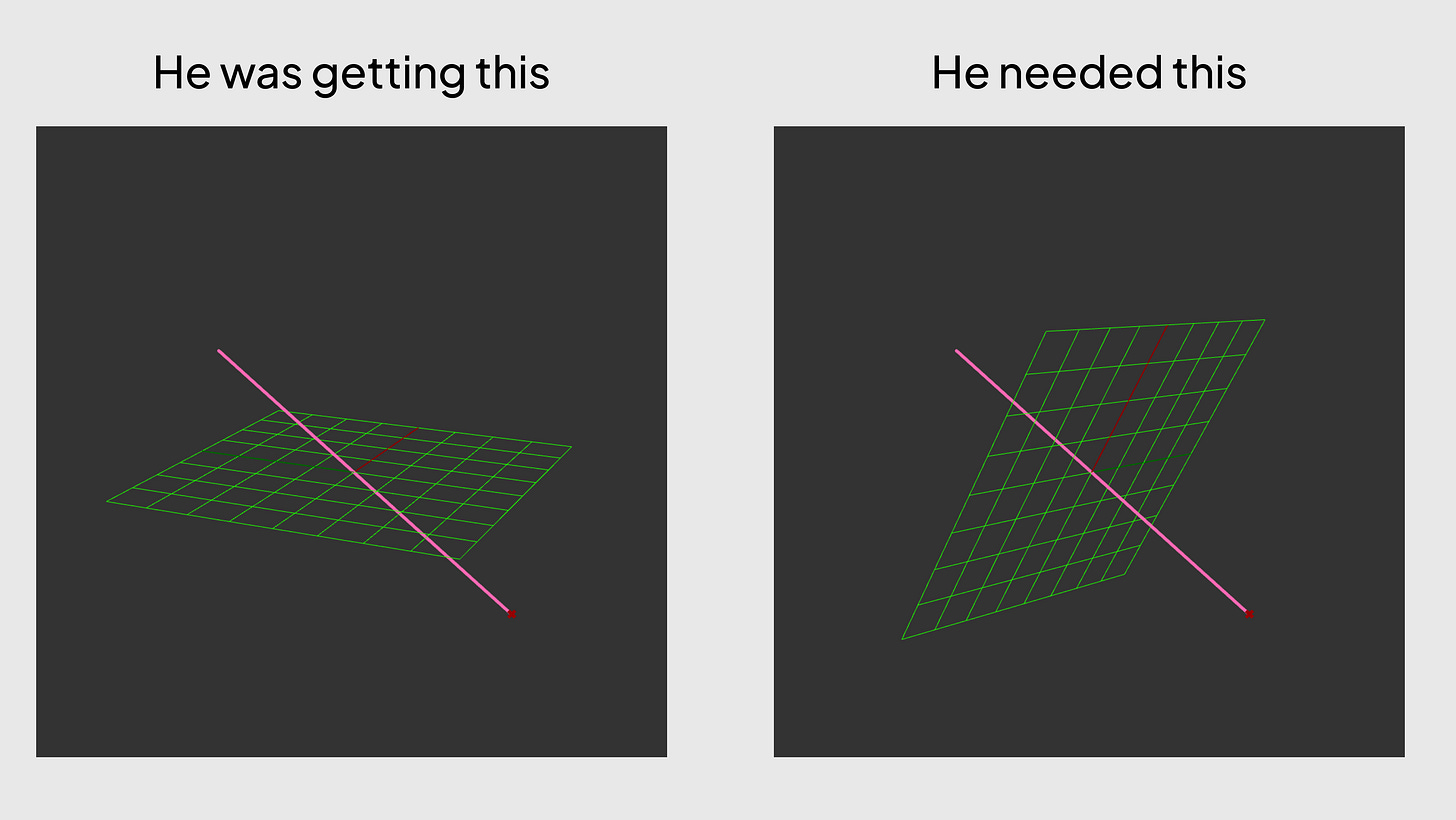
Just the other day, I watched someone struggle to create a plane in Grasshopper. The plane kept coming in flat, even though Peter wanted it at an angle. It needed to align with a diagonal line in the model.
Peter was passing points into the construct plane component in Grasshopper. But planes aren't defined by points, they are defined by vectors. When I asked him about it, he said it had always worked before. But that's only because most of his geometry before was flat. Grasshopper defaults to the XY plane when given a point. He just got lucky.
That's part of the problem. Grasshopper feels like magic. Pass in a point when it's expecting a vector, and it still works. But you don't know why it worked. You plug in something and pray it does what you want.
Grasshopper does a lot behind the scenes to make life easier. It tries to help by guessing your intent. Like when you give it a point, it assumes you want a flat plane, but that's not always the case. And if you don't understand how it works, you won't know how to fix it.
So, let's shed some light on that. Let's take a look at three numbers that form the backbone of almost every other geometry in models.
Points: Where Elements Go
Points are the anchors of your model. They define where something should be in 3D space.
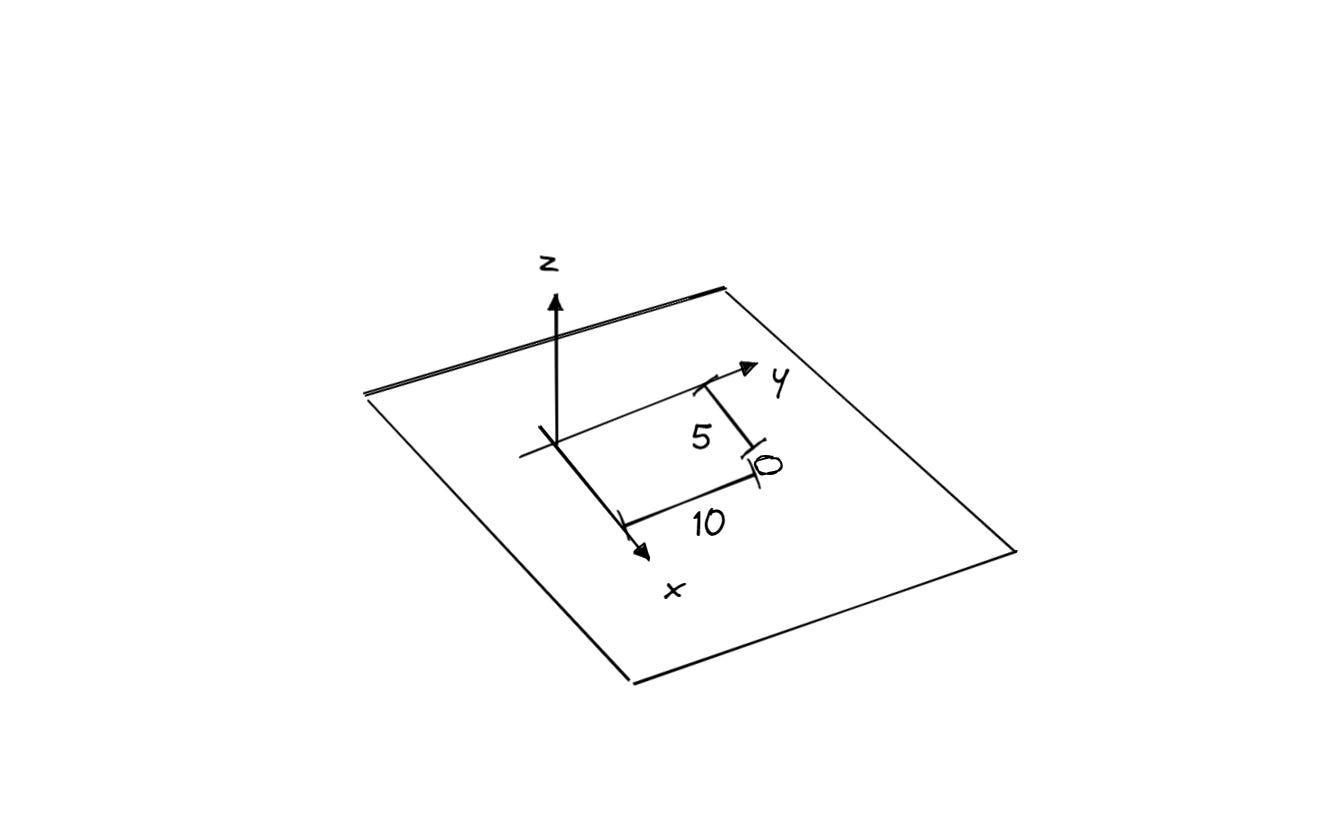
A point with coordinates {10, 10, 10} simply tells the program to place something 10 units away from the origin in each direction.
Since we work in 3D, we need to use three numbers to define a location, one for each axis (X, Y, Z). And those numbers are always relative to the origin.
Another thing to know is that most programs treat distances as unitless. To the programs, they are just numbers, to us, units are physical distances in the real world. So in a model, {10, 10, 10} could mean 10 meters or 10 feet or even 10 millimetres. It all depends on the units you're working with in your project. All the computer cares about is the number 10. It means when you're modelling, you should be consistent about the units you're using.
Points themselves are simple. They are a numerical way to define a location. But they’re the building blocks for everything else:
Curves are sequences of points.
Surfaces are made from curves in two or more directions.
Solids are made from multiple surfaces
Meshes are made from points and lines
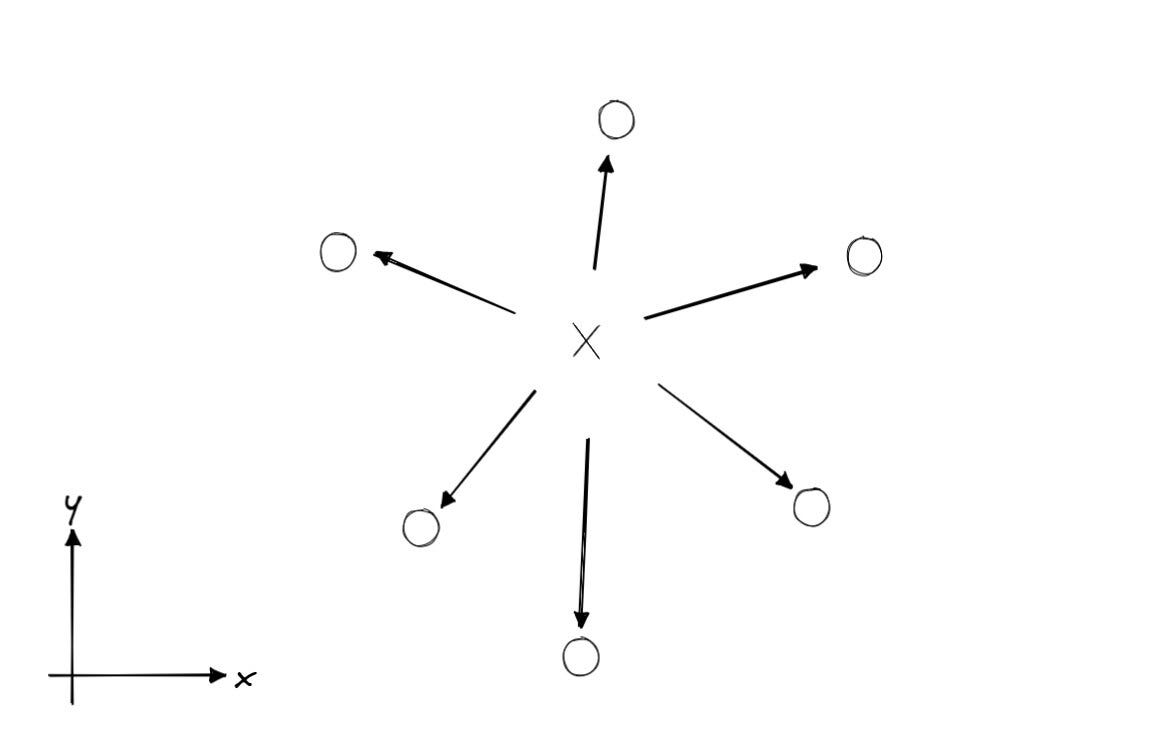
Vectors: Where Elements Face
Vectors and points are made of the same stuff, three numbers, but instead of positions, they define the orientation of elements. Vectors have a direction and a magnitude. And much like points, they are always relative to the origin.
A vector that is {0, 0, 1} is actually a vector that points from {0, 0, 0} to {0, 0, 1}. The vector {0, 0, 100} also points in the same direction, but is a 100x further. That length is the vector's magnitude.
That's important when you want to move (translate) something, you do so with vectors. The vector tells you how far and in what direction. If you wanted a pure direction, then you have to use a unit vector. That's when a vector has a magnitude of 1.
Vectors are more complex than points, mainly because the math gets more complicated. But that complexity also gives you more options. You can do operations like cross products, dot products, and vector projections, all essential operations in computational modelling.
If you wanted to read more, Hopific has a great explanation : Mastering Vectors in Grasshopper - The Complete Guide - Hopific
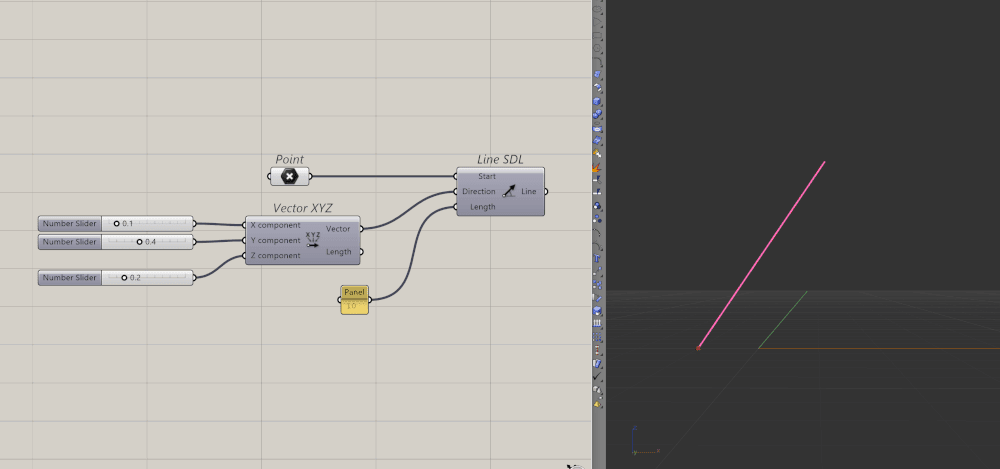
Lines = Point + Vector
Normally, a line is defined by two points. A start and an end. But you can also use a point and a vector to create a line. Think about it like putting a starting point and then "moving" the point by that vector.
In Grasshopper, that’s what the SDL (Start-Direction-Length) component does, you give it:
A starting point
A vector (which way to go)
A length (how far to go)
And Grasshopper draws the line for you.
This is one of the clearest examples of how points = location and vectors = direction. This is an extremely useful component because as we will explore in later articles, lines can be used as infinite rays that make for very useful tools when calculating intersections.
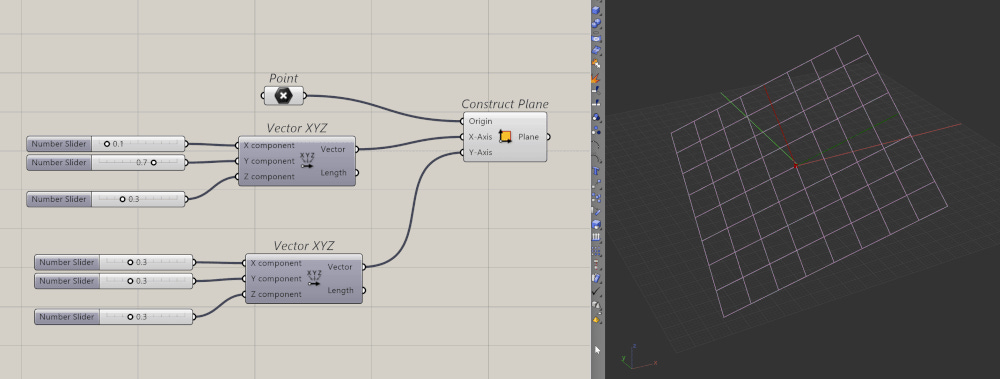
Planes = Points + Two Vectors
Back to Peter's problem, planes. If a line is “point + vector”, then a plane is “point + two vectors”. Actually, planes are made of three vectors, X, Y, and Z. But if you already have your X and Y vector, then the cross product of the two will give you your Z vector. This is also known as the normal of the plane.
In Grasshopper, you can see this in action using the Construct Plane component.
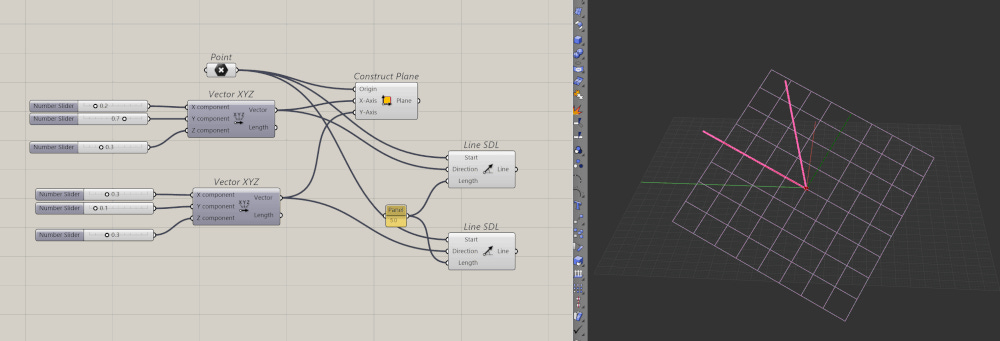
Oh one thing to note here is that your X and Y vectors should be perpendicular to each other (90° apart). But even if they aren't, Grasshopper will still try to create the plane out of the closest perpendicular vectors from your X vector. But that also means the resulting plane will be unpredictable, so it's best to always be explicit with your vectors.
Here is exactly what I mean.
The pink lines are the vectors that I am giving the Construct Plane component and the pink plane is the actual plane was made by Grasshopper. You can see that the pink lines aren't perpendicular but Grasshopper still made a plane anyways.
Again, Hopific also has an in-depth explanation about planes in Grasshopper : Construction Planes in Grasshopper - The Complete Guide - Hopific
Final Thoughts
Points and vectors are simple things to know but to use them is a lot harder. It's easy to know that points are just numbers in the X,Y,Z direction. But how do you create one from an angled plane ? What happens if you have a different coordinate system like a polar rather than cartesian ?
It is still three numbers, but the skill comes from knowing how to create and use them to solve your problems.
And if you can put in the time to practice and get to know them better, Grasshopper becomes a lot less mysterious. You won’t be surprised when a plane is slanted the wrong way. You’ll understand what’s happening behind the scenes and know how to fix it.
Thanks for reading! Subscribe to get more articles like this directly into your inbox. You’ll also get a gift from me as a thank you.