A Simple Guide to Meshes in Computational Design
This article is part of the basics of Computational Design series. Even if you don’t use Grasshopper or Dynamo every day, understanding the fundamentals can help you spot where they might be useful in your work.
Part 1 : The three vital numbers in computational design
Part 2 : A Beginner’s Guide to Curves in Computational Design
Part 3 : How Surfaces Really Work in Rhino and Why That Matters
Part 4 : What Are B-reps in Rhino, and Why Do They Matter?
Part 5 : A Simple Guide to Meshes in Computational Design (here)
When I first started learning geometry as an engineering student, we didn’t talk about curves or B-reps. Everything was points, lines, and meshes. A model didn’t need to look like real life, it just needed to be accurate. We were only interested in the physics of the model.
Back then, I never really questioned what a mesh was. It was just a bunch of points and lines feeding into equations. It felt like something the software needed to calculate the physics of something.
But over time, I started to appreciate how elegant meshes actually are. Using just points and lines, a mesh can represent any shape in real life. That’s pretty incredible. And "meshing" (the art of creating meshes) can get really complicated. The math behind generating and manipulating meshes is wild. All from just points and lines.
It took me a few more years as a computational designer to truly understand how important meshes are. I used to think meshes were only for technical people or engineers, and that B-reps were simpler to work with. But the truth is, you cannot escape meshes if you work in 3D. They are everywhere and they're incredibly useful.
What is a mesh ?
At its core, a mesh is made of points called vertices. Then you have lines that connect these points making the edges. And when the edges are connect in a loop, they form faces.
These connections are called the connectivity of the mesh.
Every face in a mesh is just a loop of edges connected through vertices. The number of edges per face defines what kind of mesh it is.
It can feel like a lot at first, but a mesh is just points → edges → faces. Once you understand that, you’re most of the way there.
Why use meshes?
So why all this complexity? Why go through the trouble of points and lines? Why not just use surfaces or B-reps?
Because meshes are fast and light.
By using only points and lines, they take up less storage space. It's also easier for a computer to work with points and lines rather than potentially complex B-rep equations.
It’s why meshes are used everywhere, from 3D analysis models to game engines to 3D viewers. They may not be as pretty or editable, but they’re extremely efficient.
Mesh Types
Like curves, meshes come in different types depending on the number of edges per face:
Quad mesh - Each face only has 4 edges (Quad is short for quadrilateral)
Tri mesh - Each face only has 3 edges (Tri is short for triangular)
n-gon mesh - Each face can have varying amount of edges (n-gon is short for a combined work of nth and polygon)
tri-quad mesh - is technically a "n-gon mesh" but it's a mesh with tri and quad faces.
Like any geometry, the quality and type play a big role in how you can use them later on. A clean quad mesh, for example, is much easier to work with than a messy n-gon mesh.
Get my free guide on how to apply computational design at work
Meshes in Rhino / Grasshopper
You can create meshes easily in both Rhino and Grasshopper.
In Rhino, the mesh command turns any B-rep into a mesh. But by default, you'll get a mix of quad and tri faces. If you want only quads, you can use QuadRemesh command, which gives you a nicer looking mesh. (this was because the QuadRemesh command didn't exist before Rhino 7)
To create a mesh in Grasshopper, you can either plug any surface or B-rep or even a closed planar curve into a mesh component. There are also components for tri and quad meshing.
Meshes vs B-reps
We know that meshes are lighter weight and more performant but they also behave differently to B-reps. Here are three key differences that matter when it comes to working with them in Rhino
Boolean Operations
Rhino supports boolean operations for both B-reps and meshes. But mesh booleans can be more fragile.
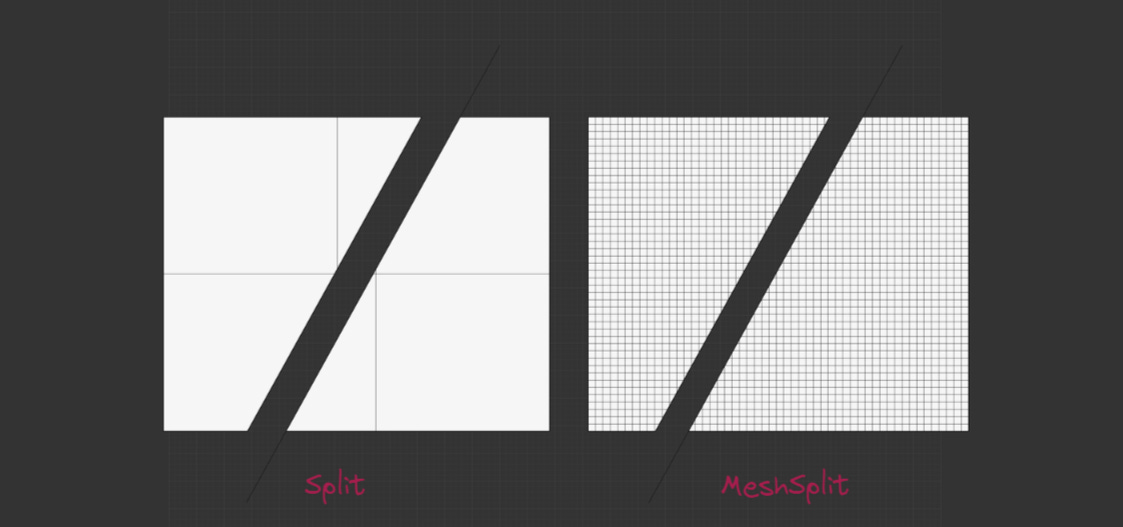
For example, try splitting a B-rep vs a mesh. The mesh, depending on its structure, may create messy triangles or fail altogether. In Rhino, you can split a B-rep with the Split command and a mesh with the MeshSplit command.
Still, it’s impressive that Rhino can reconstruct new mesh faces during operations like this. You just have to be cautious, especially on complex meshes.

Smoothness
Meshes are only ever made from straight lines. So they’ll never be truly smooth like B-reps, which are based on curves.
You can increase the mesh resolution to mimic smoothness, but you it adds more weight to the mesh, making it harder to edit.
Like any other geometry type, you want to have the minimal amount of information in a mesh while still keeping a decent resolution of the shape. Like curves, you can keep adding points to make a polyline smooth, but at some point you are better off just using a curve.
Editing
Editing B-reps is usually easier. You only need to move the control points and the whole thing updates.
Editing a mesh is much harder. Since a mesh is made off points, you have to find and select the correct points to move.
Final Thoughts
Meshes are a foundational geometry type. They're lightweight, performant, and everywhere. Yes, they’re harder to edit and not as smooth as B-reps, but they are extremely useful. Especially in computational design where you can use scripts to control most of the geometry.
Most 3D models you’ll find online are meshes. Most simulations use meshes. Most rendering engines use meshes. So if you’re working in 3D, you need to understand them.
Thank you for reading, I hope you have a better understanding of how meshes work in Rhino.
Consider subscribing if you haven’t, it helps me know my work is useful.