How Curve Parameters Give You More Control in Grasshopper
This article is part of the Designing with Numbers series, a continuation of the Geometry Basics series. Together, they explore how computational design is shaped first by geometry, then by numbers.
Part 1 : It's not always about geometry, numbers matter too.
Part 2 : How Curve Parameters Give You More Control in Grasshopper (this article)
When you ask where something is, you usually get a single answer. You get an address or a name of the shop to punch in to Google Maps.
But in computational design, where can mean something different.
We know that points tells us the exact location of our geometry in our model. So when we ask where our surface is or where the a column is, we can give people the exact location of it.
But when we look at curves and surfaces, where is also about how far along that geometry you are.
It's a bit like driving from home to the office. If your manager asks where you are, you could tell him your GPS coordinates (37.7749, -122.4194), or you could say you're "about halfway there". Both are technically correct, one is "absolute" and the other is relative to the drive itself.
Parameters is our way of telling how far along you are on a specific geometry. It's a way of describing a location without needing the XYZ values.
The reason for using this is the same as real life, it's sometimes a lot easier to find things relatively than it is through pure coordinates.
And that is what today's article is about. How curve parameters work, why they're useful and how you can use them to get more out of curves in Grasshopper.
Note: if you aren't familiar with domains then you might want to read this first
Curve Parameters
The key to understanding locations, of anything, not just parameters, is that everything is relative to something. Even the XYZ coordinates that we think are "absolute" is always relative against 0,0,0 which is typically the origin for most programs.
I say most because programs like Revit actually let you change the origin for a model. Which means you can have points that are not relative to 0,0,0. But I'm getting ahead of myself.
For now, keep in mind that anything location-wise is always relative.
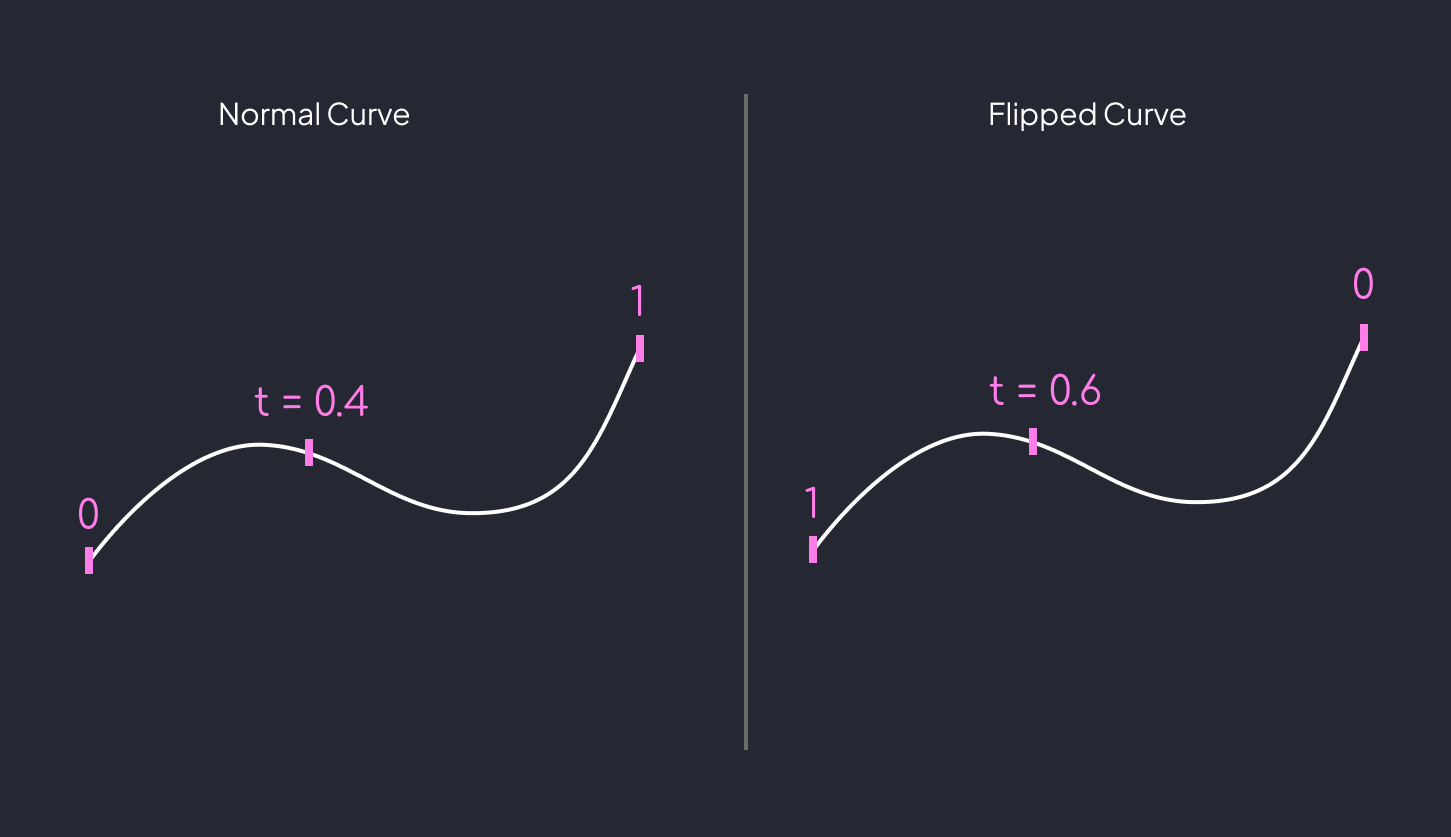
The reason it's important, is because where a point is on a curve is always referenced from it's starting point. Not the model's, the curve's. This means the direction of the curve is now important.
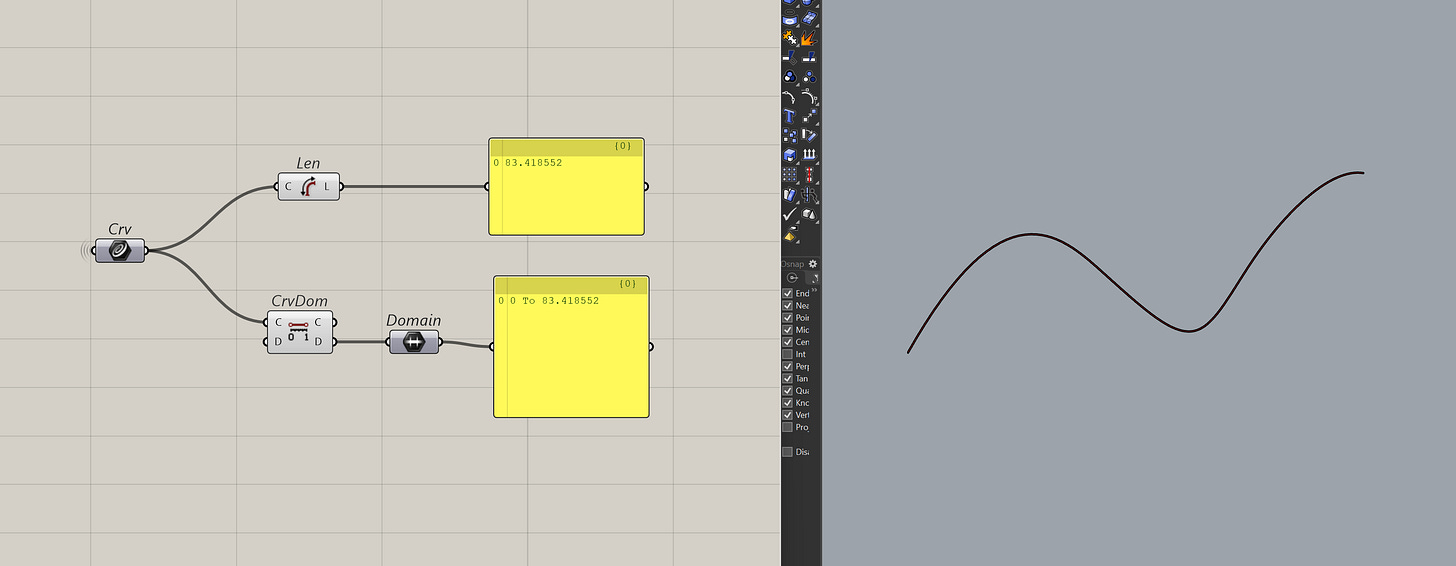
Now, typically t has a domain of 0 to the length of the curve. But as we will see soon, it's annoying to deal with because we don't always know what the length of the curve is.
And Grasshopper typically retains the original t when you split the curve. That means even if the curve is chopped in half, you still have to feed the original curve length to get the right location which is all sorts of confusing.
The reason we don't want this is because, we need a unique t for each curve and that is a pain to handle. Instead, we want a consistent way to extract information from any curve.
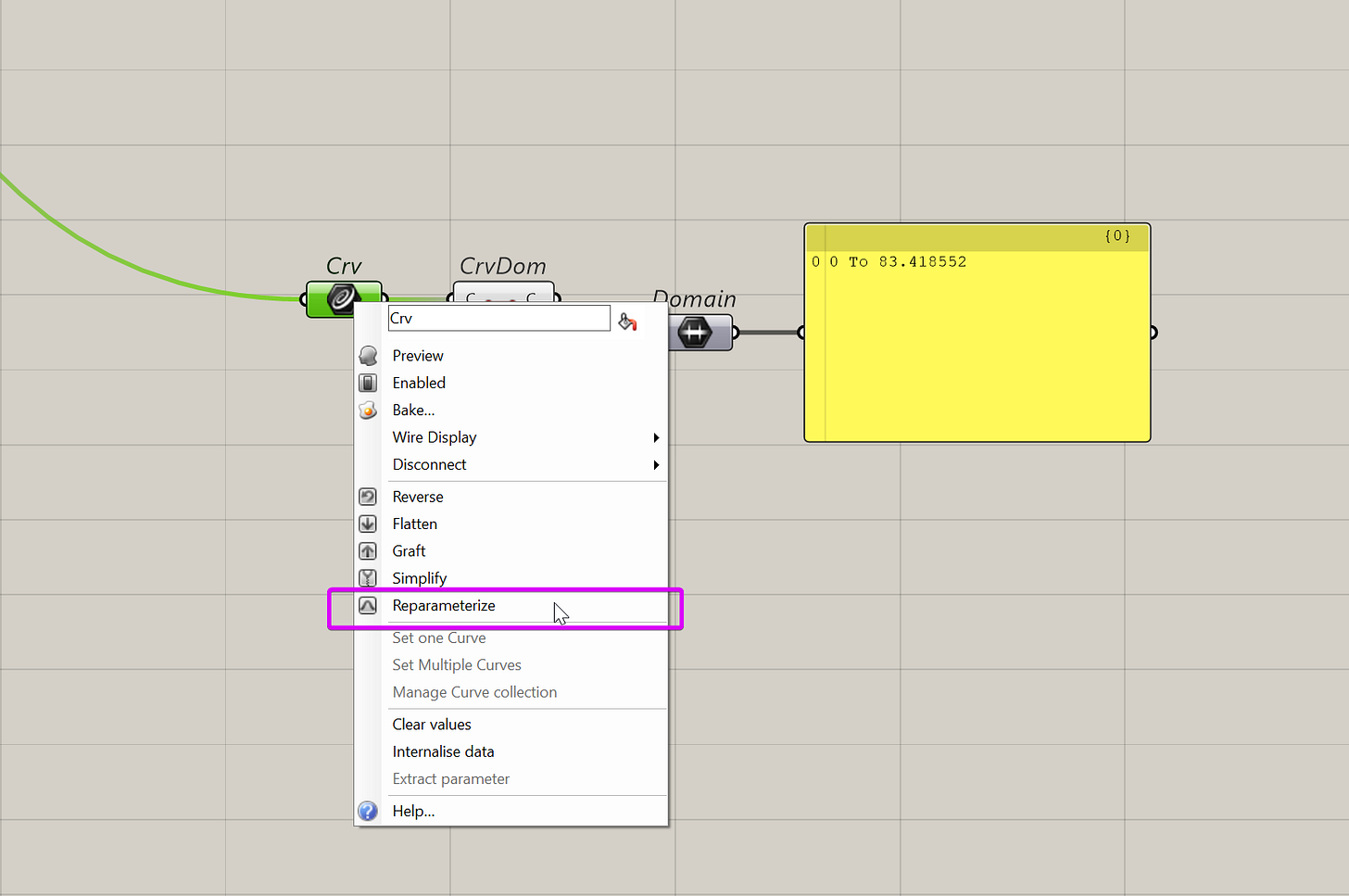
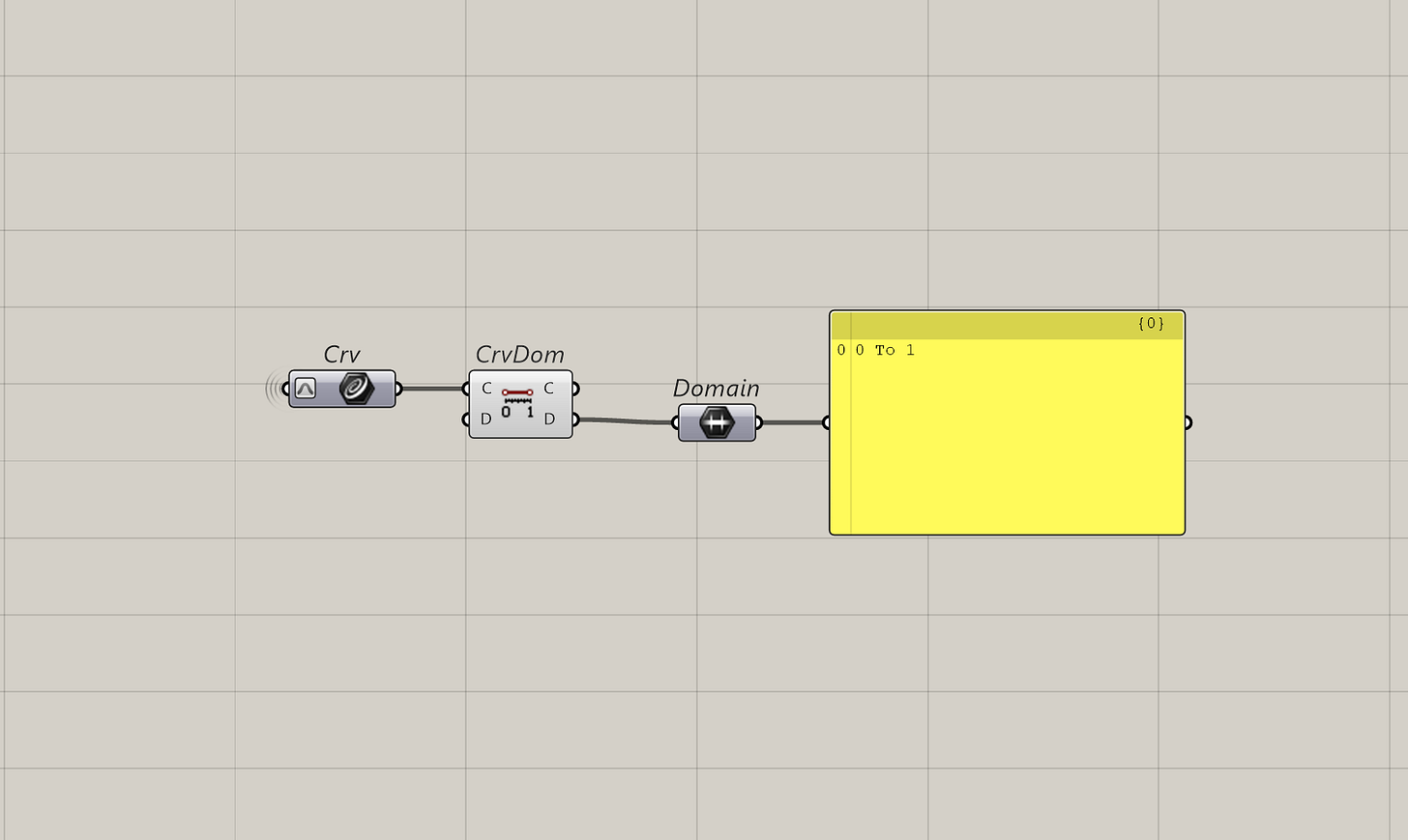
To help with that, you can re-parameterize the curve. Which turns the t into a domain of 0 To 1.
You can even do this by right-clicking on any curve input/container and setting the re-parameterize flag.
You'll then get a symbol indicating the curve has been re-parameterize.
This let's anyone easily traverse the curve without knowing it's length. It also means, a t of 0.5 is the mid point of any curve regardless of length. It's a consistent way to extract the information from curves.
Let's now take a deeper look at how to get and use these parameters to make the most out of curves in Grasshopper
Getting Curve Parameters
Curve Closest Point
Grasshopper let's you find a point on a curve that is closest with another point by using the Curve Closest Point component.
What's useful about this component is that it outputs the t of the curve. This t as we will see soon comes in really handy.
Curve Proximity
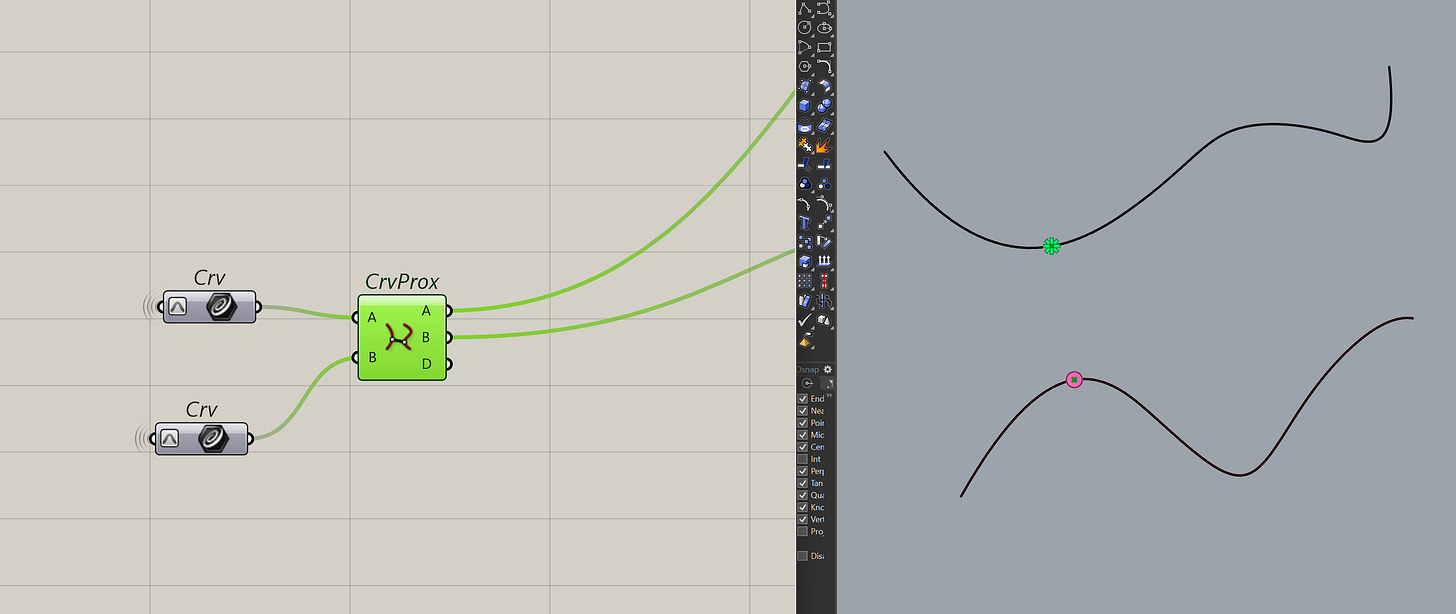
Okay, if you don't have points. You can also find the pair of closest points between two curves using the curve proximity component.
This component will give you a pair of the closest points between Curve A and B. Funnily enough, it doesn't return the ts but you can get this by using the curve closest point component from before.
Curve Intersections
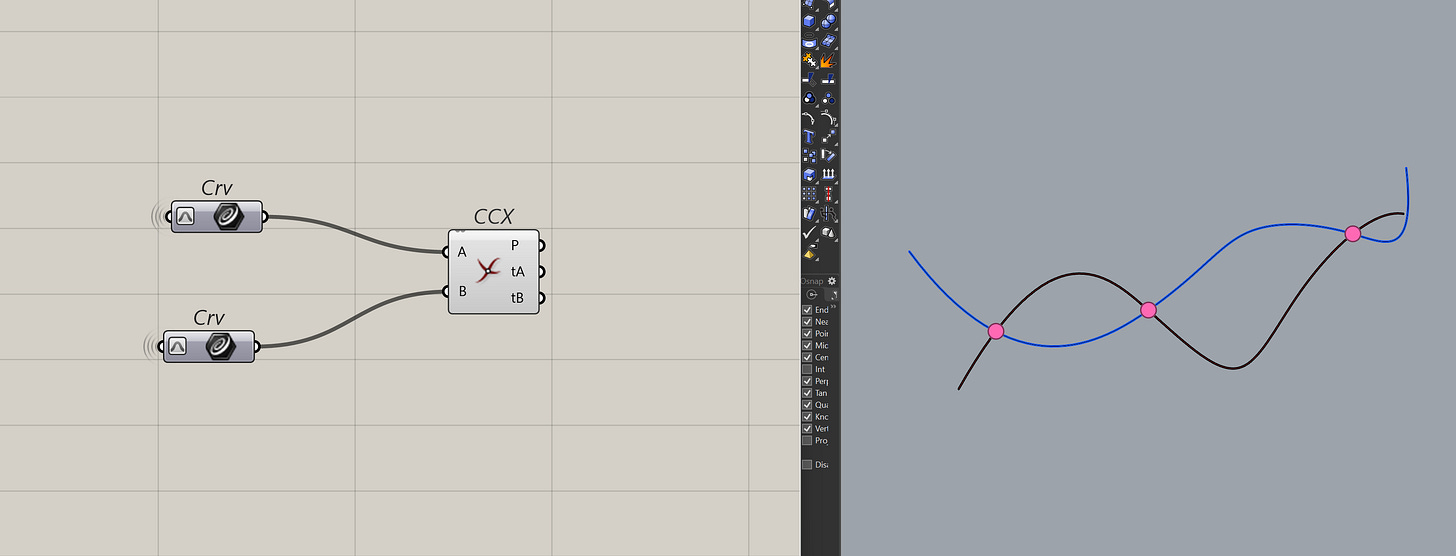
Another way to get t is through intersections. There are many intersection components that return the t of the curve. Like take this curve | curve intersection component.
This component will give you all the intersection points and the ts for both curves. Most intersection components in Grasshopper that has curves will return a t .
Alright, with that let's have a look at how to actually use these ts.
Using Curve Parameters
Getting Curve information
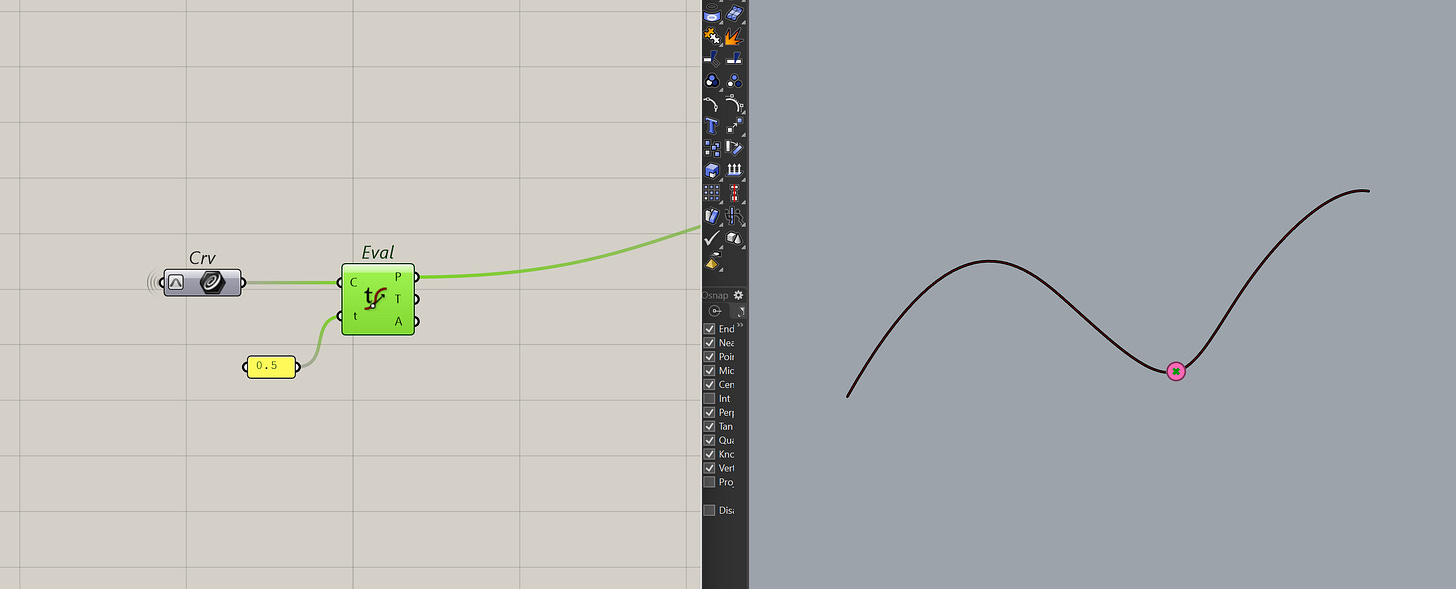
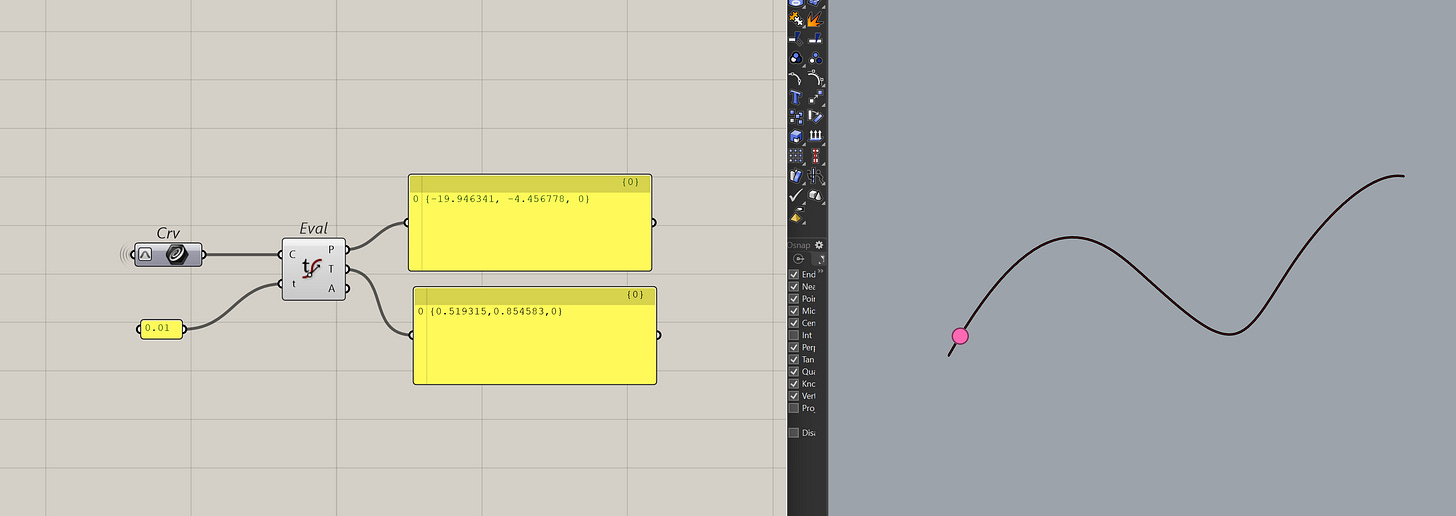
The easiest way to use t, is to extract some information at a point on a curve. You can do this with the evaluate curve component which we briefly saw at the beginning.
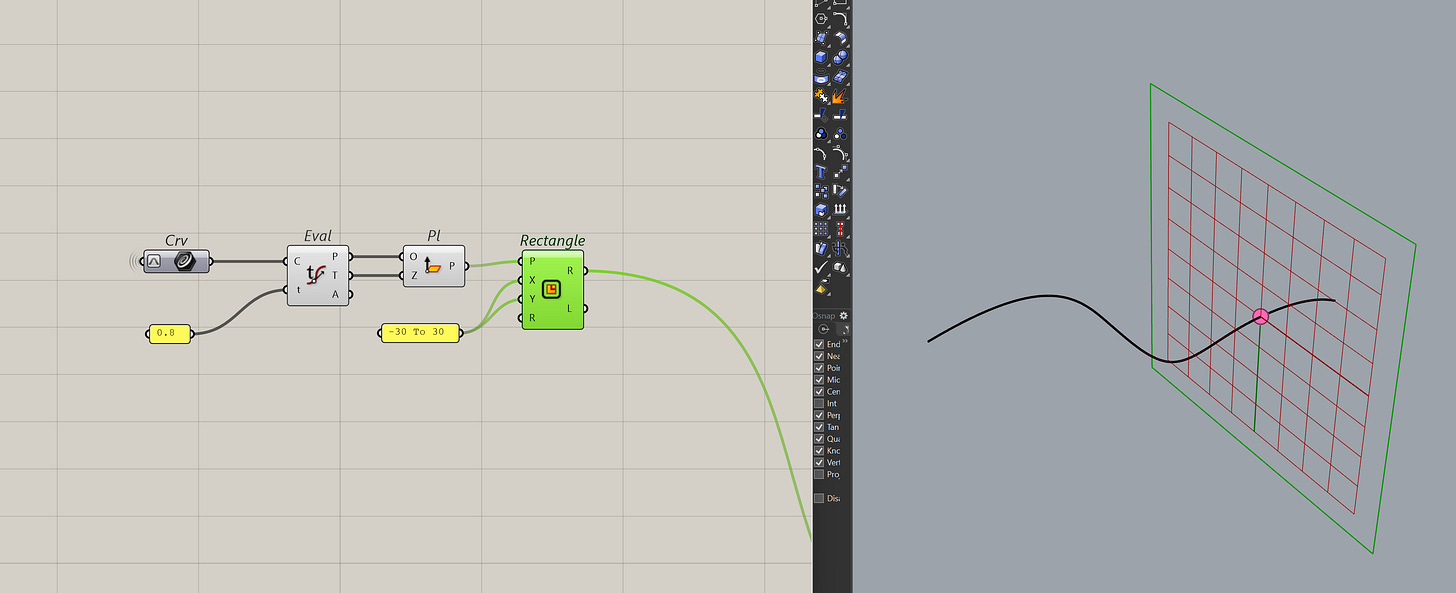
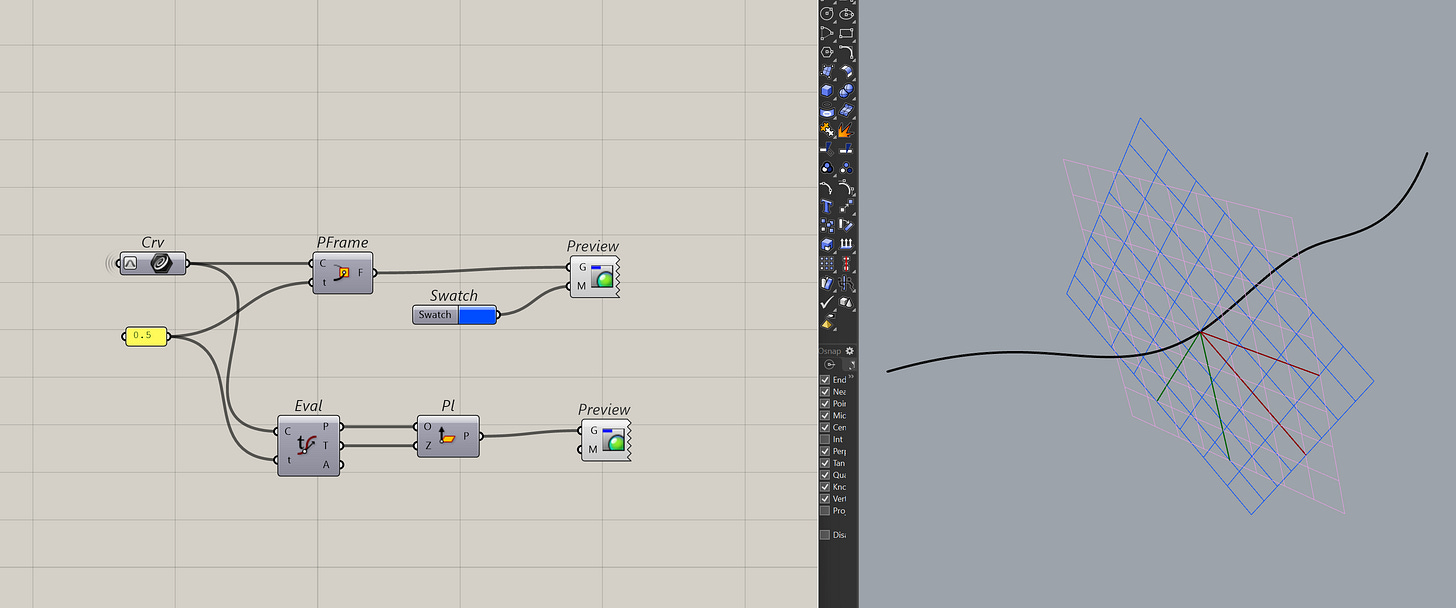
The main benefit of this component is to get the tangent vector at that point. It's useful for many reasons, one of which is using it to build planes or orient geometry.
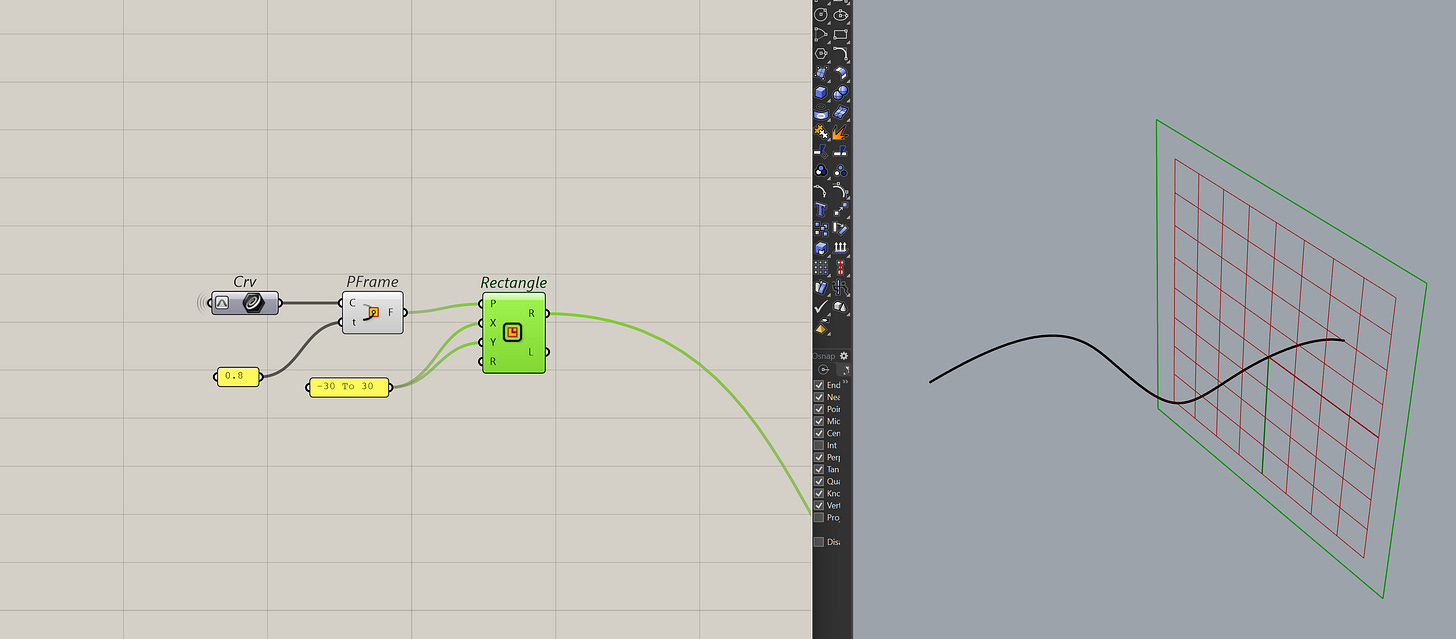
You can also use the perp frame component to get the frame at that t.
But it's not as consistent as just making the plane myself, especially, when you have curves in 3D.
Curvature
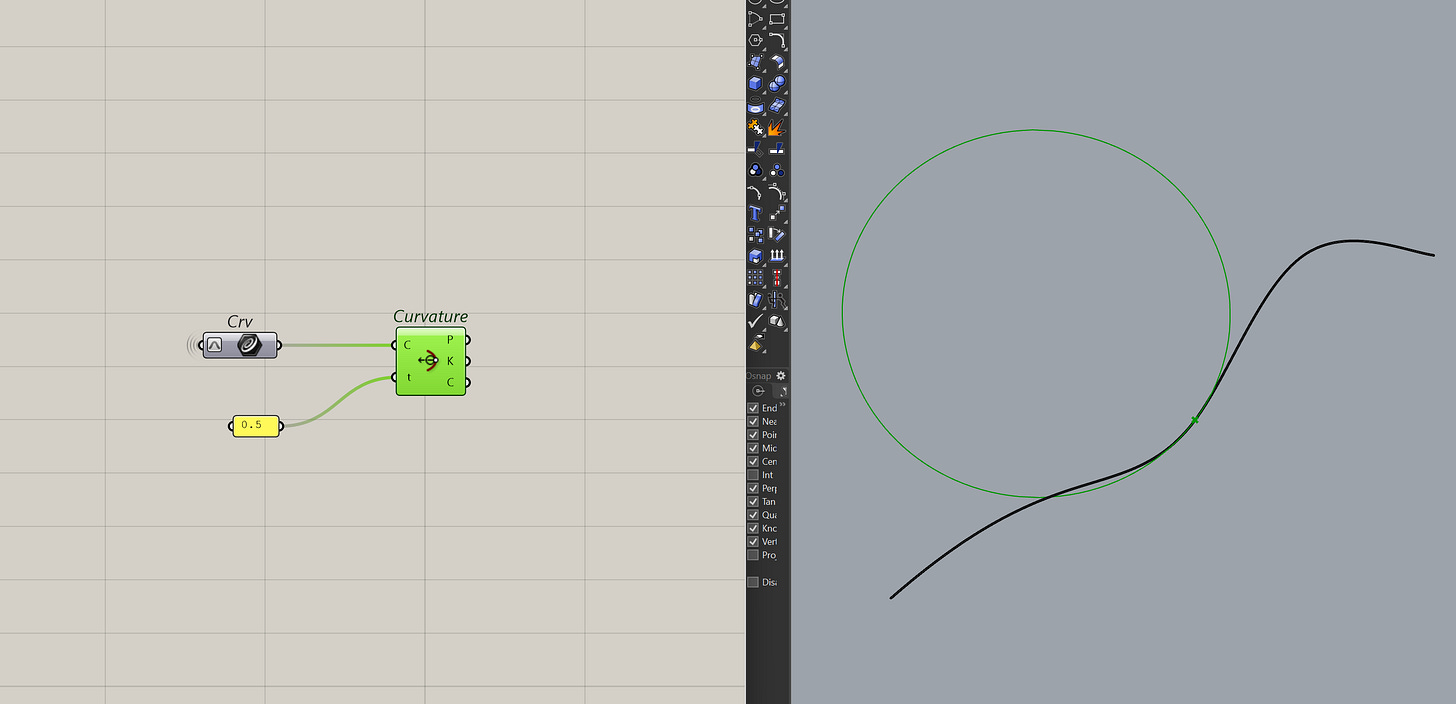
Another useful information is the curvature of a point on the curve. It's not used that often apart from seeing how the curve is behaving.
In Grasshopper, you can do this with the curve curvature component.
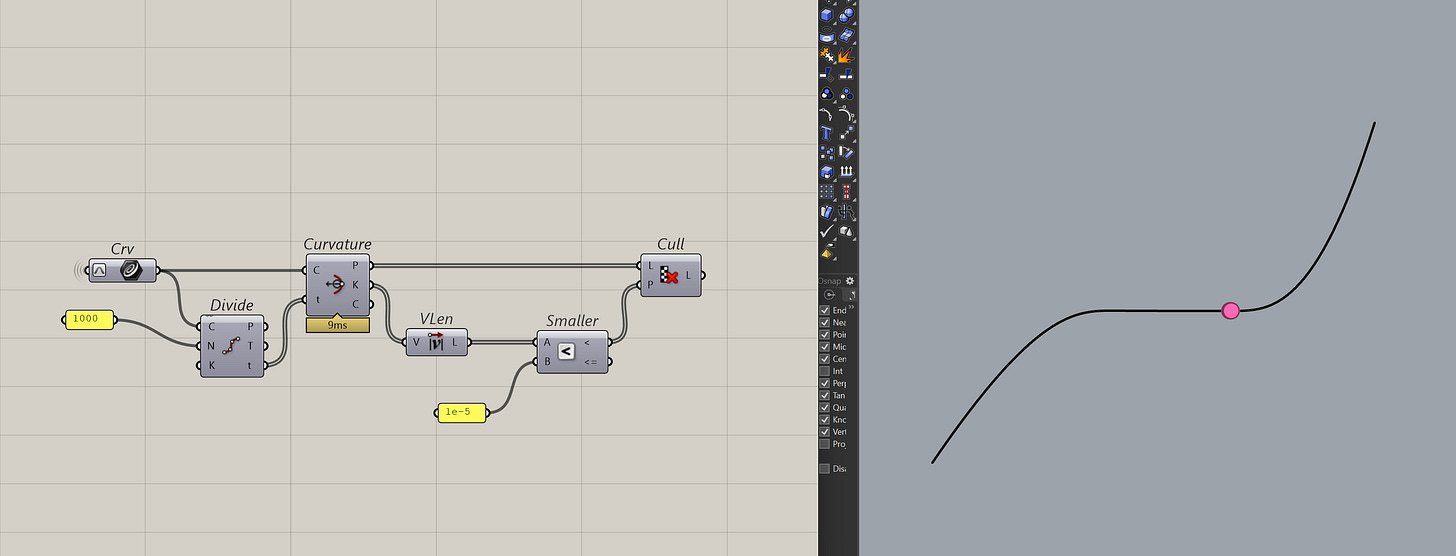
It's a bit more advanced but one way I use this component is to find a point on the curve where the curvature = 0. I normally do it for intersections or if I am trying to just extract that point.
Splitting Curves
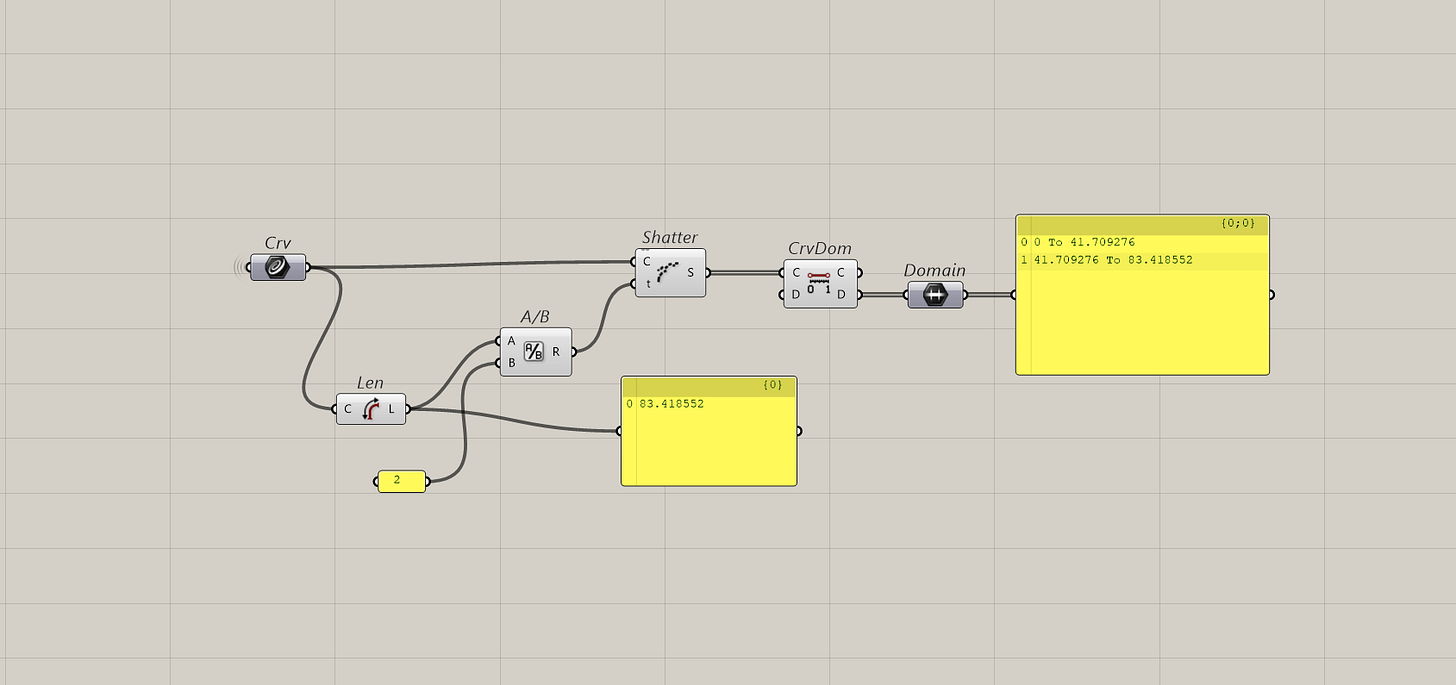
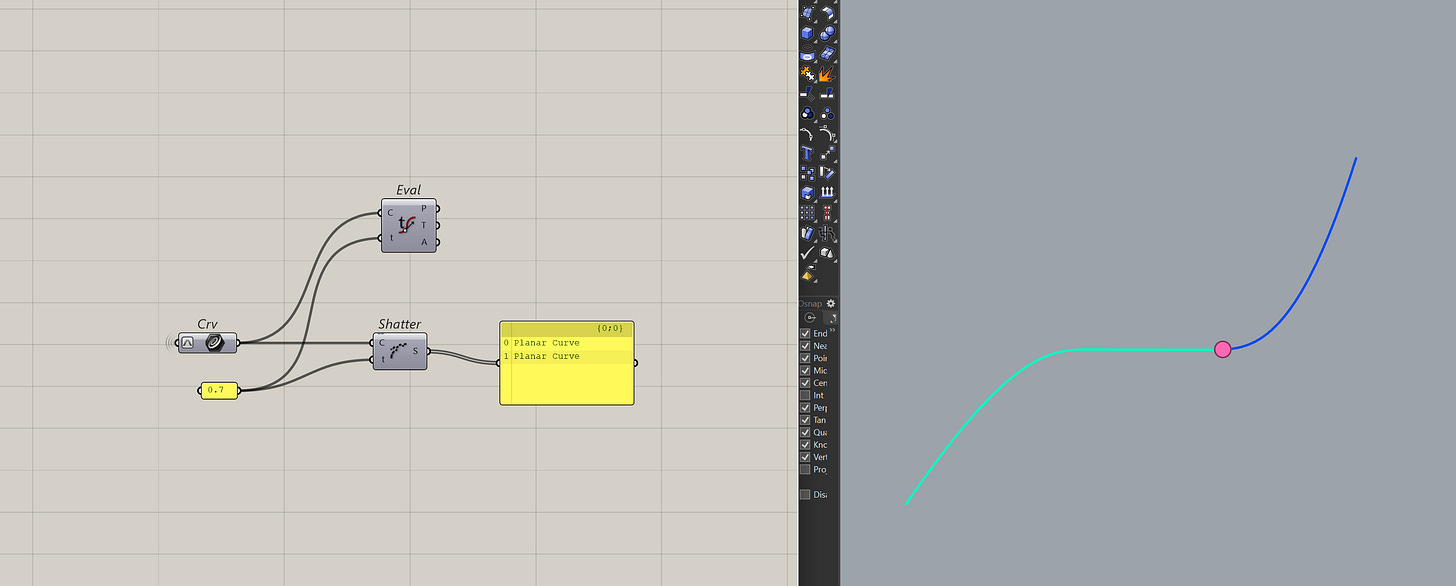
Well another useful thing about t is splitting curve. Something I do almost all the time. This is done with the shatter component.
Note: the shatter component doesn't maintain order. So, make sure to order the results by something (length, distance, etc.).
Re-Parameterize
Okay, just a note here. So far, we've talked about ts and never once on re-parameterization apart from a brief mention at the start. This was intentional because I didn't want to bog you down with the details while we were finding and using the parameters.
Just to recap, re-parameterization turns the t or any curve into a domain of 0 To 1.
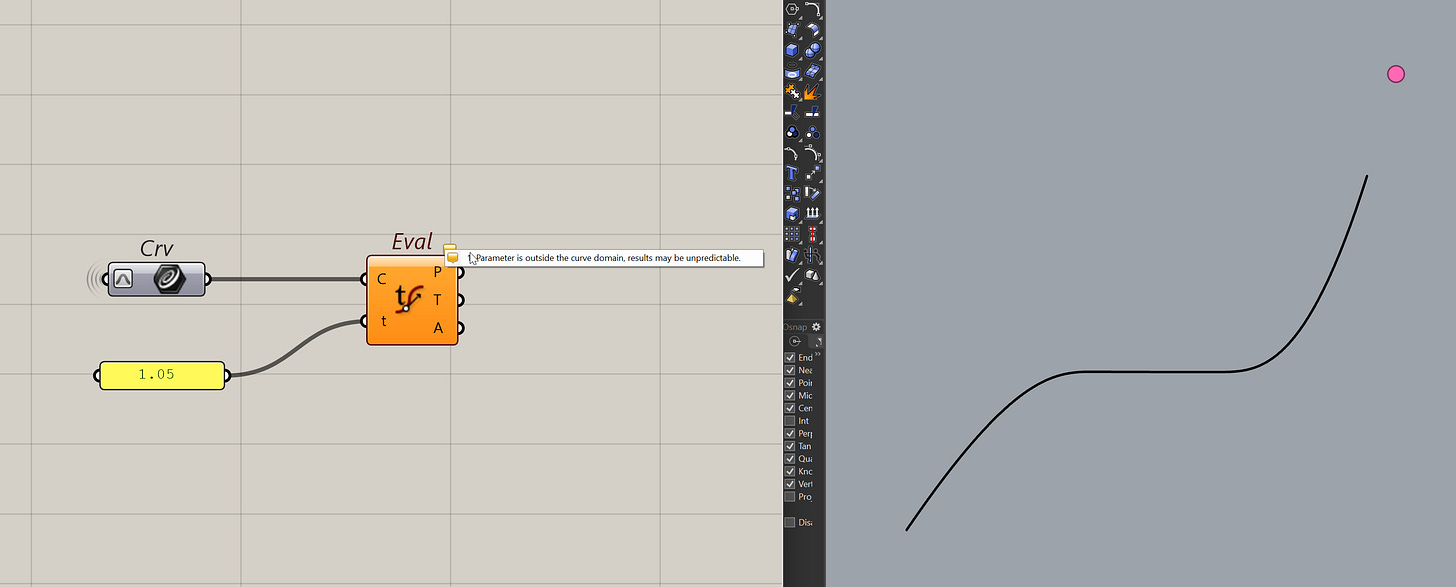
This is important because that means all the components (shatter, evaluate curve, ....) expects an appropriate t value. That means if you pass in anything more than 1 for a re-parameterized curve, you will get some weird results. For some reason Grasshopper will not error out, instead it will just return wrong results.
And that re-parameterize toggle is really small and is only applied per component which makes it really easy to miss.
My advice is to use a curve container and just re-parameterize at the beginning. This keeps the curve re-parameterized for any future use.
Final Thoughts
Alright, that was a lot to take in, but curve parameters give you a powerful way to interact with curves and pull information from them. And because you can normalize them, they also give you a consistent way of working, no matter the curve’s length.
It can feel overwhelming at first, but like anything, it gets easier the more you use it. The more you model, the more you’ll see situations where working with t saves time and makes things clearer. Get comfortable with it now, and you’ll have far more control over your curves later.
Thank you for reading. Consider subscribing if you haven’t, it really helps me know my writing here is useful.